7.2.1 简单线性相关问题引入
例7.1 表7.1所示为7个省区的人均GDP(单位为元)和建筑合同的价值(单位为亿元),试计算两个变量之间的相关系数,并在0.05的显著性水平下对显著性进行检验(数据见文件“CH7 例7.1-例7.4建筑合同”)。
表7.1 数据表

通常,在相关分析中,我们先考虑数据类型,以便把相关问题归结为线性相关、等级相关或偏相关。
线性相关模块的SPSS操作示例如下。
①在录入数据后(见CH7例7.1-例7.4建筑合同.sav),单击【图形】→【旧对话框】→【散点/点状】,系统弹出散点图类型的选择对话框,我们选择“简单分布”,单击【定义】按钮。
②系统弹出简单散点图坐标定义对话框,将变量“人均GDP”放入选择框“X 轴”中,“建筑合同的价值”放入选择框“Y 轴”中,如图7.2所示。
图7.2 散点图坐标定义对话框
③单击【确定】按钮,生成两变量的散点图,如图7.3所示。从图7.3可以清楚看出,变量“人均GDP”和“建筑合同的价值”之间存在近似的正相关关系。
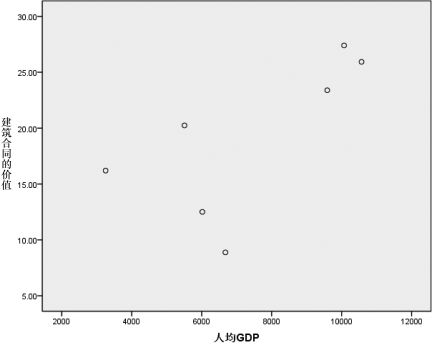
图7.3 两变量样本的散点图(https://www.daowen.com)
④单击【分析】→【相关】→【双变量】,进入“双变量相关性”对话框。
⑤在“双变量相关性”对话框(如图7.4所示)中,在左框选择要做相关分析的变量,本例选中左框的变量“人均GDP”和“建筑合同的价值”放入右边的“变量”框中。
⑥在“相关系数”区块中,选择一种相关系数。在该区块中,列出了3种相关系数供选择:a.Pearson相关系数(系统的默认值),本例选择此项,因为做相关分析的两列数据均为刻度级的数据;b.Kandall’s tau-b相关系数,它是一种依据配对样本之差的正负号的个数,计算出来的相关系数,本书略;c.Spearman等级相关系数。
图7.4 双变量相关性分析模块对话框
⑦在双变量相关性分析模块对话框的第二组选项区块,需要选择单尾检验还是双尾检验,系统默认值是双尾检验。本例可以接受系统的默认值,也可以选择单尾检验,因为从图7.3中,可以确定两个变量是正相关关系。
⑧单击【确定】按钮,系统输出结果,如表7.2所示。
表7.2 相关系数及显著性检验
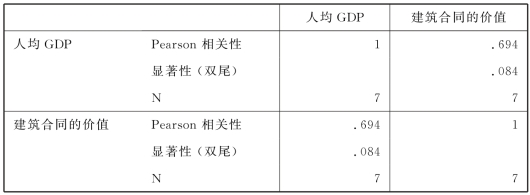
结果说明:从表7.2中可见人均GDP 和建筑合同的价值之间的Pearson相关系数为0.694,显著性概率p=0.084>0.05,说明两个随机变量的相关系数是没有显著异于0的。
在图7.4中,还有一个【选项】按钮,它要求你选择输出额外的统计值(如均值、标准差等)及选择缺失值的处理方式。对于缺失值的处理方式,一般接受系统的默认值。
