7.5.1 非线性相关问题引入
若两个随机变量按照前面的方法检验出不存在显著的线性相关性,那么就没有别的信息可以推断了吗?
例7.5 打开数据文件“CH7例7.5CH8非线性相关、曲线回归.sav”,试分析变量x和y 的相关性。
按照线性相关性分析的方法,不难算出,x和y的线性相关系数为-0.005,p≈0.988,两个随机变量似乎没什么关系,但是,如果画出以x 为横坐标,以y 为纵坐标的散点图,不难发现,x 和y 存在较为明显的二次关系。至少,从直觉上,不能因为两个变量之间不存在明显的线性关系,就断言两个变量之间不存在相关关系。
①单击【图形】→【旧对话框】→【散点/点状】,系统弹出一个散点图类型的选择对话框,如图7.9所示。
图7.9 散点图类型的选择对话框
②在这个对话框中,有5种类型的散点图的选择,接受默认值“简单分布”。
③单击【定义】按钮,系统弹出简单散点图的坐标定义对话框,如图7.10所示。
图7.10 简单散点图的坐标定义对话框
④在图7.10中,分别把左框中的变量x和y用箭头送入右边的“X 轴”框和“Y 轴”框中。(https://www.daowen.com)
⑤单击【确定】按钮,系统输出散点图,如图7.11所示。从图7.11可以看出,变量x 和y 存在较为明显的二次关系,看得出y 是x 的二次曲线,图中散点的最低点的位置大约在x=3的附近,于是,推测y=(x-3)2。因此,在下一阶段做非线性变换。
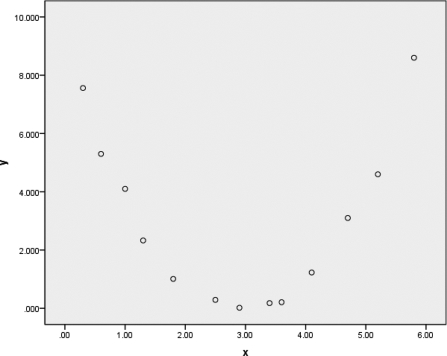
图7.11 两变量样本的散点图
⑥在数据视图窗口中,单击【转换】→【计算变量】,在弹出的对话框中,完成z=(x-3)2。预计y 与z 之间有很高的线性相关性,接下来,完成y 与x 之间、y 与z 之间的(线性)相关系数的计算。
⑦在数据视图窗口中,单击【分析】→【相关】→【双变量】,在弹出的对话框中,用箭头把变量x、y 与z 送入右框中。
⑧单击【粘贴】按钮,在弹出的语法编辑器窗口中,把第一个命令句“/VARIABLES=x y z”改为“/VARIABLES=y with z x”。注意,改动不仅仅增加了命令词“with”,而且变量x、y 的位置也变了。这样做的意义是:分别计算y 与x 之间、y 与z 之间的线性相关系数。
⑨在语法编辑器窗口中,单击绿色的三角形(“运行选定内容”按钮)。系统输出结果,如表7.6所示。
表7.6 y与x之间、y与z之间的线性相关性
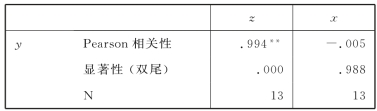
**.在置信度(双测)为0.01 时,相关性是显著的。
从表7.6的数据可以看出,y 与x 之间t 检验显著性概率为0.988,显然y 与x 不存在显著性线性相关的关系。但是y 与z 之间的线性相关系数(表7.6中的Pearson相关性)是0.994,显著性(双尾)p 值为0.000(在SPSS输出的表格中,双击这个数字,会显示更精确的值),小于0.01,这说明在0.01的显著性水平上该线性相关系数与0有显著性差异。这表明,可以推断y 与x 之间是以构造的函数形式高度非线性相关的。
