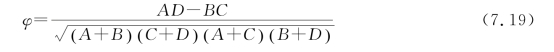7.6.2 算法原理
1.二值名义级变量与刻度级变量的相关方向与强度的测量：点双列相关系数
当一个变量是二值名义级变量，另一个变量是刻度级变量时，可以把Pearson相关系数的计算方法延伸到这里。显然，在运用Pearson相关系数公式
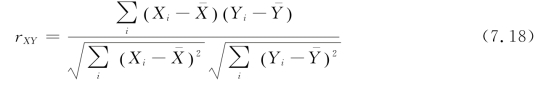
其中，
计算之前，必须解决二值名义级变量取值的刻度化问题。
设X 是二值名义级变量，在一般情况下，我们用数字0与1表示X 的两个状态的取值，本来这两个数字0、1没有任何大小的概念，仅仅是两个不同的符号，就像字母A、B 表示两个不同的状态一样，这里的0、1也仅仅表示X 的取值限于两个不同的状态。但是，如果当变量X 从一个状态转变为另一个状态时，Y 的刻度级数据有明显不同的取值倾向（如明显变大或者明显变小），那么就可以断定X、Y 是相关的。如果我们将这两个数字（或者说编码）数量化，把它们当成能够进行加减乘除运算的数据来处理，就可以用Pearson相关系数公式来表示相关的强度了。这就是所谓的点双列相关系数。
但需注意，对应于Y 的某个值，X 取值0或取值1是任意指定的，所以当对X 的取值规定交换一下后，所计算出来的X 与Y 的相关系数的符号就会变化。如果其原来为正，X 取值规定交换后，其就为负；反之亦然。
例如，设X1=0，X2=1，Y1=3，Y2=5，则
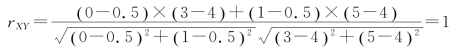
当把X 的取值规定交换一下后，X1=1，X2=0，则
不变，
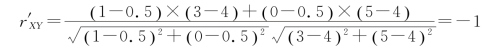
可见，
因此，点双列相关系数所反映X 与Y 的相关方向是相对的、人为指定的，其反映X 从一个指定的状态变为另一个状态时，Y 的取值倾向的特征。也就是说，改变符号并不改变点双列相关系数的本质特征。而常规的Pearson相关系数的正、负号却具有本质的意义，人们不能随意改变常规Pearson相关系数的正、负号。
因此例7.6不必担心“汉堡是否有奶酪”的取值（编码）变化会使得点双列相关系数（表7.9中的Pearson相关性）不同，因为虽然二值名义级变量赋值（0或者1）变化，但是点双列相关系数的绝对值是相同的。
但是，当名义级变量是多值时，我们不能强行把变量X 数值化以后，用普通Pearson相关系数的计算公式来解决相关系数的计算问题。因为我们既不能断定变量X 取3个以上值的顺序，也无法断定这些取值之间具有什么样的数量关系（如不同的编码间是否具有等差性），因而无法用普通的Pearson相关系数公式来解决问题。
2.两个二值名义级变量的相关方向与强度的测量：点双列相关系数
当所要考察的两个变量都是二值名义级变量时，我们可以仿照上面的做法，把二值的编码（一般用0、1）数值化，然后借用Pearson相关系数公式进行分析。
下面我们通过一个例子来说明两个二值名义级变量的相关性的分析问题。
例7.8 某市关于“抽烟与患肺病”的抽样调查结果是：不抽烟健康人员有360人，不抽烟患肺病人员有190人，抽烟健康人员有290人，抽烟患肺病人员有480人，数据见文件“CH7例7.8抽烟与肺病”。
在SPSS数据文件中，每一条记录表示一个被抽到的人，变量值有两个，一个是“是否抽烟”，一个是“是否患肺病”。打开这个数据文件后，发现它是图7.14所示的缩约格式的，所以，先要对其进行加权处理。
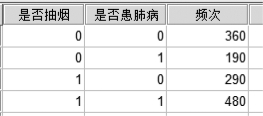
图7.14 两变量缩约格式的数据
①在数据视图窗口的菜单中，单击【数据】→【加权个案】，在弹出的对话框中，选择“加权个案”，然后把权重变量“频次”用箭头送入右边的“频率变量”框中，如图7.15所示。为了直观考察这两个变量的关系，我们用SPSS来做分组条形图。
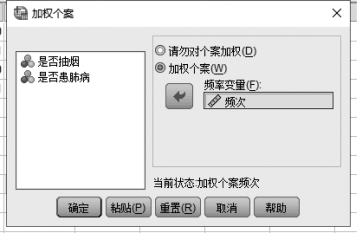
图7.15 加权个案对话框
②单击【图形】→【旧对话框】→【条形图】→【集群条形图】，图形中的数据默认选择“个案组摘要”，如图7.16所示。然后单击【定义】按钮，进入“定义堆积条形图”对话框。
③在弹出的对话框中，把变量“是否抽烟”用箭头送入“类别轴”框中，把变量“是否患肺病”用箭头送入“定义聚类”框中。
④单击【确定】按钮，就得到图7.17了。从图7.17看出，不抽烟的患肺病人数在较低的位置，而抽烟的患肺病人数的在相对高的位置。看来，两个变量可能有相关的关系。两个二值名义级变量的相关系数用φ 表示，在这种情况下其就是Pearson相关系数。
图7.16 条形图对话框
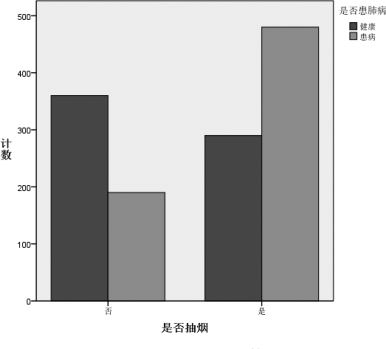
图7.17 集群条形图
⑤单击【分析】→【相关】→【双变量】，进入双变量相关性分析模块。
⑥在双变量相关性分析模块对话框（如图7.4所示）中，选中左框的变量“是否抽烟”和“是否患肺病”放入右边的“变量”框中。
⑦在该对话框的“相关系数”区块中，接受系统的默认值（Pearson）。
⑧在该对话框的“显著性检验”区块中，接受系统的默认值（双尾检验）。
⑨在该对话框中，勾选复选框“标记显著性相关”。
⑩单击【确定】按钮，系统输出结果，如表7.10所示。表7.10中的数据显示，“是否抽烟”与“是否患肺病”的φ 相关系数是0.274，显著性概率是0.000（双击后看到具体数值是5.57×10-24），拒绝零假设，φ 相关系数与0存在显著性差异，也就是说，拒绝两个变量不相关的假设。
表7.10 两个二值名义级变量的φ相关系数
**.在置信度（双测）为0.01 时，相关性是显著的。
两个二值名义级变量的相关系数φ，还可以用SPSS的另一个模块计算。
①单击【分析】→【描述统计】→【交叉表格】，进入“交叉表格”对话框。
②在弹出的对话框中，选中左框的变量“是否抽烟”和“是否患肺病”，将一个放入右边的“行”框，另一个送入右边的“列”框中。
③单击【Statistics】按钮，在弹出的框中选择“Phi和Gramer V”统计量，也就是φ 相关系数，如图7.18所示。
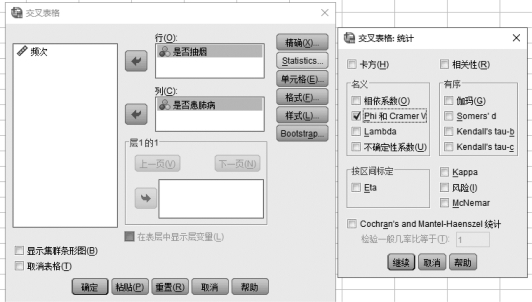
图7.18 “交叉表格”对话框
④单击【继续】按钮，回到“交叉表格”对话框。
⑤单击【确定】按钮，系统输出结果，如表7.11所示。
表7.11 φ相关系数的计算结果
其结果与通过直接单击【分析】→【相关】→【双变量】，计算的Pearson相关系数相同，都为0.274。
注：这里的正、负号是无关紧要的，因为改变任何一个二值名义级变量取值的编码位置时，φ 相关系数的符号都会改变但其绝对值不会变，读者可以试着自己证明一下。
另外，两个二值名义级变量的相关系数φ，也可以在设置变量（如图7.19所示）后用式（7.19）进行计算。
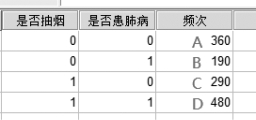
图7.19 两变量缩约格式的数据
