8.1.1 输入式线性回归问题引入
我们先来看一个一元线性回归的例子。简单地说，一元线性回归指的是只研究一个自变量和一个因变量之间的统计关系。
例8.1 研究我国31个省区市的“人均食品支出”对“人均收入”的依赖关系（数据文件为“CH8例8.1例8.2一元与多元回归”）。
设“人均食品支出”用随机变量Y 来表示，“人均收入”用随机变量X 来表示，那么这道题所求的两个变量之间的不确定关系可以用式（8.2）来表示。
其中：“人均食品支出”Y 是被解释变量；“人均收入”X 是解释变量；β1是待估参数（截距项）；β2是待估参数（斜率项，反映了X 的边际效益）；u 是随机干扰项，与X 无关，它反映了Y 被X 解释的不确定性。
如果随机干扰项u 的均值为0，那么对式（8.2）两边在X 的条件下求均值，有
反映出从“平均”角度来看的确定函数关系。
我们可以先从SPSS的操作方面来看看这个问题是怎么解答的。
①录入数据，单击【分析】→【回归】→【线性】，系统弹出一个对话框。
②在该对话框的左栏中选择变量“人均食品支出”，单击向右的箭头，将其放入“因变量”框中。在左栏中选择变量“人均收入”，单击向右的箭头，将其放入“自变量”框中，如图8.1（a）所示。
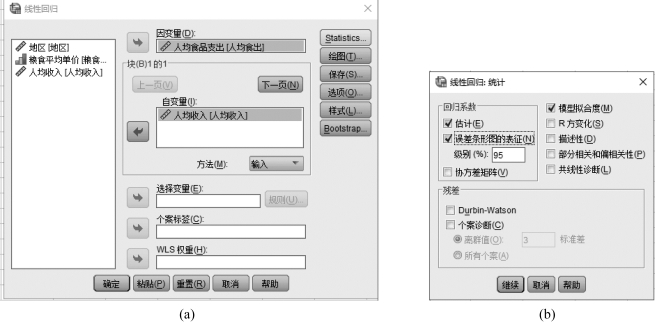
图8.1 一元线性回归对话框
③单击窗口右侧的【Statistics】按钮，弹出一个新的对话框，如图8.1（b）所示。在“线性回归：统计”对话框中的“回归系数”区块中，有以下3项选择。
a.估计：这是系统的默认值。选择此项，系统会输出回归系数B、B 的标准差、标准系数贝塔、B 的t值及其双尾检验的p 值。
b.误差条形图的表征：复选项。选择此项，系统会输出每一个B（非标准化回归系数）的95%的置信区间。本例选择此项。
c.协方差矩阵：不选择。单击【继续】，回到线性回归对话框。
④单击【确定】按钮，系统输出结果。
下面对结果进行分析。
表8.1给出了线性回归的方法是输入法，参与的自变量（已输入变量）为“人均收入”，表的下方标出的因变量为“人均食品支出”。
表8.1 一元线性回归已输入/除去变量a
a.因变量：人均食品支出
b.已输入所有请求的变量。
表8.2给出了R（复相关系数，此处即简单相关系数）、R 平方（判定系数R2）、调整后的R 平方
标准估算的错误
（估计标准误差）。
表8.2下方的“预测变量”也称为“外生变量”，在对因变量（被解释变量）做预测时，首先要预测出外生变量的值，所以称为“预测变量”。
表8.2 模型总体参数表
a.预测变量：（常量），人均收入
表8.3是方差分析表，给出了方差分析的结果。该表第1列给出了总变差的来源：回归、残差和总计（总计为回归和残差之和）。该表第2列为“平方和”，分别为回归行对应的变差（就是已解释变差）、残差行对应的变差（就是残差平方和）、总计行对应的变差（就是总变差）。该表第3列为“自由度”（回归行对应的自由度是k-1，残差行的自由度是n-k，总计行对应的自由度是k-1+n-k=n-1）。该表第4列为“均方”，为前面两列相除，即“平方和”除以“自由度”。该表第5列为“F”，即方差检验F 值。该表第6列为“显著性”，为F 值的显著性概率值。
表8.3 方差分析表
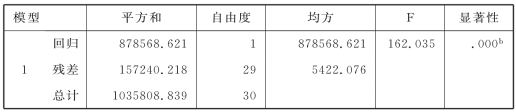
a.因变量：人均食品支出
b.预测变量：（常量），人均收入
表8.4是回归系数及显著性检验表，该表第一列是对模型的解释变量的说明。第二列包括非标准化的回归系数
、“标准误差”为
的标准误差Sj。第三列为标准系数贝塔。第四列为t值。第五列为t值的显著性概率p 值。在本例中，常数项的t检验不通过，p=0.458＞0.05，即对应的系数与0 无显著性差异。自变量“人均收入”的t检验通过，p=0.000＜0.05，即相应的系数显著异于0。第六列是B 的95.0%置信区间。
我们看完了例8.1这样一个“简单”（简单指的是SPSS的操作过程）的一元回归的例子后，很自然地会想到，SPSS程序背后的算法步骤是什么？专有名词的含义是什么？原理又是什么？
表8.4 一元线性回归的回归系数及显著性检验表a
a.因变量：人均食品支出