7.1.1 相关系数的种类
若相关系数是根据总体全部数据计算的,则称为总体相关系数,记为ρXY;若是根据样本数据计算的,则称为样本相关系数。
1.两个随机变量的总体(线性)相关系数
定义7.1 在概率论中,通常用协方差Cov(X,Y)和相关系数ρXY来衡量两个随机变量X、Y 的取值之间相互关系的程度和方向,其计算公式分别如下:
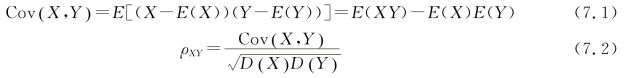
其中,ρXY是一个无量纲的量,称为随机变量X、Y 之间的相关系数。可以证明,相关系数是区间[-1,1]之间的一个量。若ρXY=0,则称X 与Y 不相关。
若X 与Y 相互独立,由概率论的知识我们可以知道Cov(X,Y)=0,即ρXY=0,X与Y不相关。反之,若X 与Y 不相关,则X 与Y 不一定相互独立。
但不相关的两个服从正态分布的随机变量是相互独立的。
2.两组样本的线性相关系数
定义7.2 设![]() 是(X,Y)的一组样本,则样本的线性相关系数为
是(X,Y)的一组样本,则样本的线性相关系数为
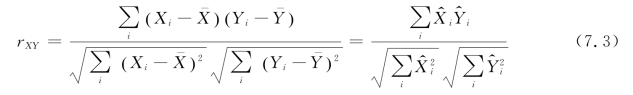
其中,![]() 称为样本(Xi,Yi)的中心化处理结果,这里的数据是刻度级的数据。
称为样本(Xi,Yi)的中心化处理结果,这里的数据是刻度级的数据。
样本相关系数是对总体样本间的线性相关关系的描述,这种相关系数也称为Pearson积矩相关系数,通常简称为Pearson相关系数(皮尔逊相关系数)。样本相关系数也是区间[-1,1]之间的一个量。
3.两组样本的等级相关系数
在实际应用中,有时获得的原始资料没有具体的数据表现,只能用等级来描述某种现象,要分析现象之间的相关关系,就只能用等级相关系数。
等级相关系数又称为“秩相关系数”,是反映等级相关程度的统计分析指标。常用的等级相关系数有Spearman等级相关系数和Kendall等级相关系数等。(https://www.daowen.com)
定义7.3 设(X1,Y1),(X2,Y2),…,(Xn,Yn)是总体(X,Y)的一组顺序级数据样本,则样本的Spearman(斯皮尔曼)等级相关系数为
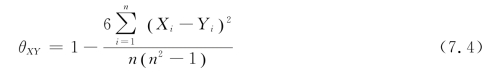
由于刻度级数据也具有顺序级数据的特征,因此,引申出带有刻度级数据样本的等级相关系数的概念。
定义7.4 设![]() 是总体(X,Y)的一组刻度级的数据样本,设RXi为Xi的名次,RYi为Yi的名次,
是总体(X,Y)的一组刻度级的数据样本,设RXi为Xi的名次,RYi为Yi的名次,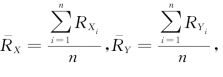 则可以用如下方式求出等级相关系数:
则可以用如下方式求出等级相关系数:
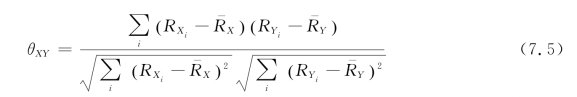
当两组样本值中,有一组是顺序级的数据,另一组是刻度级的数据时,也可以计算等级相关系数,只需把刻度级的数据用相应的名次来表达就行了。
在SPSS中,求数据名次的操作是单击【转换】→【个案等级排序】。
4.样本的偏相关
偏相关指的是,在诸多相关的变量中,剔除了(控制了)其中的一个或若干个变量后,两个变量之间的简单相关关系。例如,控制了年龄和工龄的影响,看工资收入和受教育程度之间的关系;或者剔除了销售能力的影响,研究销售量和广告费用之间的关系。
定义7.5 已知变量X、Y、Z 是彼此有关联的一组变量,那么,在剔除(控制)了变量Z的影响之后,变量X、Y 的偏相关系数为
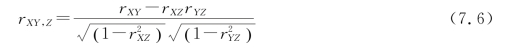
其中,r··表示Pearson积矩相关系数,r··,·表示偏相关系数,下标中逗号“,”之后的变量是被控制的变量,逗号“,”前面的变量是被计算偏相关的两个变量。
定义7.6 已知变量X、Y、Z1、Z2是彼此有关联的一组变量,那么,在剔除(控制)了变量Z1,Z2的影响之后,变量X、Y 的偏相关系数为
![]()
其中,r··,·是控制了一个变量的偏相关系数,下标中逗号“,”之后的变量是被控制的变量,逗号“,”前面的变量是被计算偏相关的两个变量。
