6.2.2 无重复双因素方差分析算法的步骤
刚才我们看到了SPSS的操作步骤，从结果表中可以大致看到算法的步骤。在无交互作用的双因素方差分析中，由于有两个因素，所以在分析时需要将一个因素安排在“行”的位置，称为行因素A，将另一个因素安排在“列”的位置，称为列因素B。设因素A 有s 个水平A1，A2，…，As，因素B 有k 个水平B1，B2，…，Bk。行因素和列因素的每一个水平都可以搭配成一组，观察它们对试验指标的影响，共抽取s×k个数据，其结构如图6.9所示。
图6.9 无重复双因素方差分析的结构图
假设在Ai与Bj下的总体Xij～N（μij，σ2），注意这个式子相当于假设s×k个总体分布的方差都相同，但其均值可能不同。设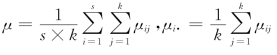
称为第i行总体的平均，
称为第j 列总体的平均。
1.假设
零假设：
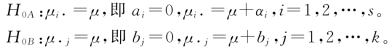
备择假设：
H1A：μ1·，μ2·，…μs·之间不完全相等（至少有两个不等），或ai不全等于0。
H1B：μ·1，μ·2，…μ·k之间不完全相等（至少有两个不等），或bj不全等于0。
2.计算
①算行间变差：
②算列间变差：
③算总误差平方和：
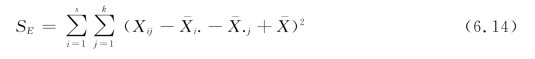
④算总变差：
其中，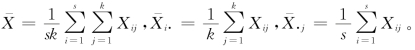
可以证明，在无交互影响的双因素模型下，有如下结论。
a.当H0A成立时，
b.当H0B成立时，
⑤计算2个方差之比：
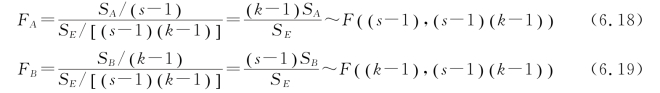
3.做假设检验
对于给定的α 查表，查出fα（（s-1），（s-1）（k-1）），若FA的样本观察值fA＞fα（（s-1），（s-1）（k-1）），或fA的显著性概率p＜α，则表明sA较大，即
的绝对值较大，对应的总体参数μi·-μ的绝对值较大，所以，以α的概率拒绝H0A，即至少因素A 中有两个水平之间的平均效果（均值），差异足够大。反之，接受H0A，即因素A 的不同水平之间的平均效果（均值）没有显著性差异。
同样，对于给定的α查表，查出fα（（k-1），（s-1）（k-1）），若FB的样本观察值fB＞fα（（k-1），（s-1）（k-1）），或fB的显著性概率p＜α，则表明sB较大，即
的绝对值较大，对应的总体参数μ·j-μ的绝对值较大，则以α的概率拒绝H0B，即至少因素B 中有两个水平之间的平均效果（均值）差异足够大。反之，接受H0B，即因素B 的不同水平之间的平均效果（均值）没有显著性差异。