6.1.1 单因素方差分析问题引入
在参数假设检验中,我们经常检验两个总体分布的均值是否相同,如果有多个总体,则必须两两比较检验,十分烦琐。而方差分析可以一次完成对多个总体的均值是否相同的检验:
![]()
方差分析本质上是研究分类型自变量对数值型因变量的影响。在分析均值之间是否有差异时,需要借助于对方差(数据误差来源)的分析,所以叫方差分析。
1.相关概念
单因素方差分析的基本思想是,用方案之间的方差(服从χ2分布)和所有方案内部的方差之和(也服从χ2分布)的比值(服从F 分布)与fα的比较,来判别s个方案的均值是否相同。
设有s个方案,各方案的试验效果如表6.1所示,问怎样判断这s个方案的效果是否有显著区别(即在一定的显著性水平下判断这s个总体均值是否相同)?
表6.1 单因素方差分析模型表
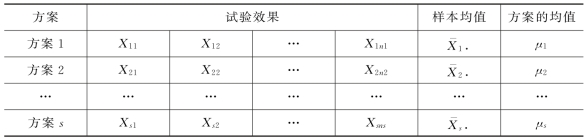
这s个方案可以是s 项政策,其中Xij是被访问人j 对政策i起作用大小的评分;也可以是s个阶层的人对同一个问题的评分,其中Xij是第i层中的第j 个人对该问题的评分;还可以是s台设备、s种药品、s种饲料、s种工艺、s种材料等的效果。
显然,这里不同方案的数据是相互独立的。
所谓单因素,就是指只有“方案”这个变量(因素)。不同方案就是“方案”这个变量的不同取值。
单因素方差分析的目的,就是一次性地检验各个方案的均值是否相同:
![]()
单因素方差分析所使用的统计量是F 统计量。
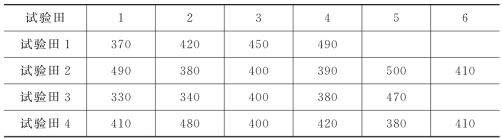
例6.1 已知在一组给定的条件下种植油菜所得亩产量(单位为斤)服从正态分布。某农场欲检验4块试验田对油菜亩产量的影响是否不相同(假定经过检验表明不同试验田下的油菜产量方差相等)。为此,某农场将4组初始条件完全相同的油菜种子,在完全相同的其他种植条件下,分别在4块试验田种植。所得到的亩产量数据如表6.2所示。试分析不同试验田下的油菜亩产量是否存在显著性差异(α=0.05)?
表6.2 4块不同试验田的油菜亩产量情况
 (https://www.daowen.com)
(https://www.daowen.com)
通常,在方差分析中,我们把对试验结果发生影响和起作用的自变量称为因素。如果方差分析研究的是一个因素对于试验结果的影响和作用,就称为单因素方差分析。在本例中,因素就是可能影响油菜亩产量的不同试验田。因素的不同选择方案称为因素的水平。本例中试验田有4种不同的选择,也就是说因素有4个水平。因素的水平实际上就是因素的取值或者因素的分组。例如,在施肥量、光照时间、灌溉时长、商品包装、质量、价格和产地等方面取不同的值或将其分为不同的组,就表示因素选了不同的水平。方差分析要检验的问题就是因素选不同的水平,对结果有无显著的影响。若无显著影响,则随便选择哪一种方案都无所谓;否则就要选择最终油菜亩产量最多的一种试验田方案。
①试验。在工程管理或科学研究中,试验是为了解因素对工程质量或科研指标的影响而进行的,试验的目的是取得样本数据。例如,工程质量管理中,进行混凝土浇筑强度试验、机械碾压土强度试验、路基抽样试验等。也可以通过试验观测或调查的方法进行试验数据,如定位时间、测距误差、尺寸观测、调查登记等,即此处的试验为广义的试验。
②因素。因素指试验中考察的对象,如浇注方案、填土方案、机械性能、水泥掺量、碎石掺量等,或网络节点定位问题中的时间误差、角度、深度、某参数等。
③水平。考察一个因素对试验的影响时,通常将其控制在几个不同的状态或等级上,这些不同的状态或等级称为水平,如A 因素的A1,A2,…,An水平,以及B 因素的B1,B2,…,Bm水平。
④指标。通常把生产实践与科学试验中的结果,如产品的性能、产量等,统称为指标。
2.比较均值模块的SPSS操作示例
我们接下来看看例6.1用SPSS怎么解答,打开数据文件“CH6例6.1试验田”。
①在打开数据文件“CH6例6.1试验田”后,单击【分析】→【比较平均值】→【单因素ANOVA】,进入单因素方差分析模块。
②在单因素方差分析模块(如图6.1所示)中,选中左框的变量“亩产量”放入右边的“因变量列表”框中。
③选中图6.1中左框的变量“试验田”放入右下部的“因子”框中,如图6.1所示。
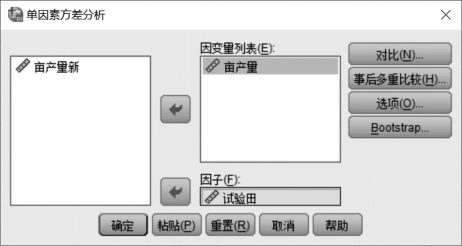
图6.1 单因素方差分析模块
④单击【确定】按钮,系统输出结果,如表6.3所示。
表6.3 方差分析表

⑤结果说明:表6.3的第一列是方差来源,说明是来源于组间的,还是组内的。表6.3的第二列是变差(样本与均值的离差平方和),第二行第二列的组之间变差也就是对应于εij(即Xij-μi)的误差项平方和。第三列是自由度(s-1=3,n-s=17,n-1=20)。表6.3的第四列是均方,是变差除以相应的自由度,即离差平方和的均值。表6.3的第五列是统计量F 的值f,是组间方差与组内方差之比,组内方差反映的是线性模型Xij=μi+εij的误差项的状况。表6.3的第六列是f 统计值的显著性概率(外侧概率p),用于显著性检验。此处,p=0.412>α=0.05,所以,在0.05的检验水平下,认为不同试验田下的油菜亩产量不存在显著性差异。
