5.2.1 双尾单样本Z检验
设总体X~N(μ,σ2),本节介绍有关μ的参数假设检验。先来看情况一:已知方差σ2,检验原假设H0:μ=μ0,备择假设H1:μ≠μ0;或原假设H0:μ≥μ0,备择假设H1:μ<μ0;或原假设H0:μ≤μ0,备择假设H1:μ>μ0。
下面我们先看一个例子。
例5.4 根据长期经验和对资料的分析,某袋装糖果的重量X 服从正态分布,方差σ2=1.21。随机抽取6袋该袋装糖果,测得其重量(单位为g)如下:32.56、29.66、31.64、30.00、31.87、31.03,检验这批袋装糖果的平均重量为32.50 g是否成立(α=0.05)?
解:步骤1:从题意出发,判定是双尾检验还是单尾检验,写出原假设和备择假设。
由题可知,1袋袋装糖果的重量大于32.5 g,或者小于32.5 g都不好,所以是双尾检验,假设H0:μ=32.5,H1:μ≠32.5。
步骤2:选取一个合适的统计量,计算出这个统计量的值。
选取的统计量一般要满足如下条件:
①已知其分布和参数(从而可以得出水平轴上任何一点右侧的概率);
②在题目的条件下,能够算出这个统计量的值。具体而言,这个统计量应当包含所要检验的参数μ(代入假设值后为μ0)和与之对应的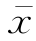 ,以及已知的σ2或σ,以便由样本观察值计算出这个统计量的值来。
,以及已知的σ2或σ,以便由样本观察值计算出这个统计量的值来。
由第4章的定理可知

Z 就满足上面的①、②两个条件。
代入题目中的已知条件,求得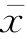 =31.13,σ=1.1,因为主要遵循使犯弃真错误的概率足够小的原则,所以在假设H0:μ=32.50成立的条件下先计算出
=31.13,σ=1.1,因为主要遵循使犯弃真错误的概率足够小的原则,所以在假设H0:μ=32.50成立的条件下先计算出![]()
步骤3:建立检验规则。建立原则是令犯弃真错误的概率很小,为α。
如果H0正确,则样本X1,X2,…,X6来自正态总体X~N(32.5,1.21)。
方法1:临界值法。
根据检验水平α,查表确定临界值zα/2,使
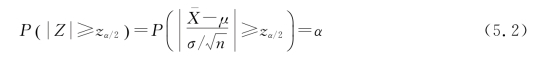 (https://www.daowen.com)
(https://www.daowen.com)
整体判断思路是使犯弃真错误的概率很小。如果H0是正确的,那我们在什么情况下会“弃真”?“弃真”也就是拒绝总体均值是32.5的假设。当然在由样本反映出来的样本均值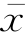 偏离32.5太多的时候,我们会更倾向于认为总体均值也偏离32.5太多。那怎样判断?判断依据就是上面的式(5.2)。在H0为真的前提下,使拒绝H0事件的概率很小,即P
偏离32.5太多的时候,我们会更倾向于认为总体均值也偏离32.5太多。那怎样判断?判断依据就是上面的式(5.2)。在H0为真的前提下,使拒绝H0事件的概率很小,即P![]() ,也就是使犯弃真错误的概率很小,为α。
,也就是使犯弃真错误的概率很小,为α。
现在的问题是如何确定临界值zα/2?有以下两种方法。
①查概率统计类教科书后面的附表。在附表中,zα/2对应的是累积概率为0.975的标准正态分布的临界点。
②用SPSS计算。打开任意一个数据文件,然后单击【转换】→【计算变量】→【逆DF】→【IDF.NORMAL(0.975,0,1)】,如图5.2所示,可以得出zα/2≈1.96。
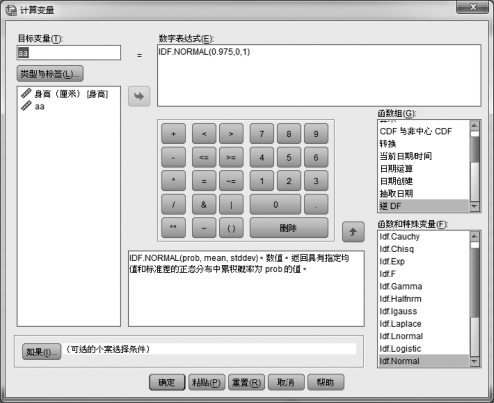
图5.2 用SPSS求临界值
为什么临界植标识为zα/2?因为在概率统计学里大多遵循这样的规则,即使用临界值右侧的概率值作为这个临界值变量的右下角标。
方法2:p 值法。
根据步骤2中求出的z≈-3.05,它左边的概率的2倍就是对应的p 值。利用SPSS计算,过程如下:打开任意一个数据文件,然后单击【转换】→【计算变量】→【CDF 与非中心CDF】→【2*CDF.NORMAL(-3.05,0,1)】,如图5.3所示。可以得出z的p 值约为0.0023。
步骤4:做出判断。
由临界值法可知,![]() 成立,小概率事件发生,最后下结论否定H0,即不能认为这批糖果的平均袋装重量是32.50 g。
成立,小概率事件发生,最后下结论否定H0,即不能认为这批糖果的平均袋装重量是32.50 g。
由p 值法(如图5.4所示)可知,如果α=0.05,由Z 服从N(0,1)分布的图形很容易知道,zα/2右侧的面积(概率)应当为0.025,-zα/2左侧的面积(概率)也应当为0.025,当z 在zα/2的右侧或在-zα/2的左侧时,在z 的密度函数N(0,1)图上,z 就远离32.50,所以拒绝μ=32.50的假设。
显然此时,若μ=32.50正确,我们拒绝它的概率只有0.05。由上一步知,z 的p 约为0.0023,这和![]() 是一致的。因此,由p 值≈0.0023<0.05,得结论否定H0,即不能认为这批糖果的平均袋装重量是32.50 g。
是一致的。因此,由p 值≈0.0023<0.05,得结论否定H0,即不能认为这批糖果的平均袋装重量是32.50 g。
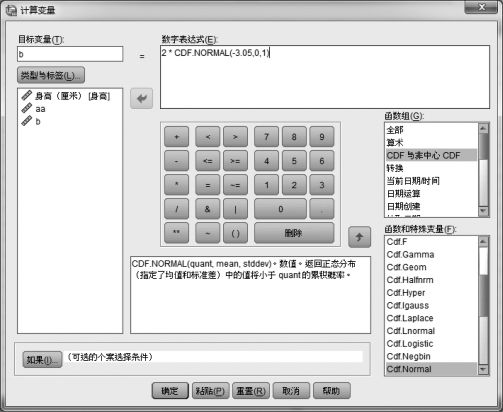
图5.3 用SPSS求p值
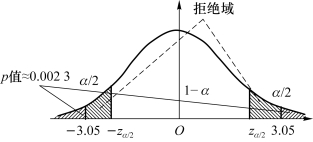
图5.4 例5.4的p值法图示
