4.1.3　基于一般正态分布的几个重要统计量的分布

4.1.3　基于一般正态分布的几个重要统计量的分布

设X1，X2，…，Xn是正态总体N（μ，σ2）的一个随机样本，则样本均值函数和样本方差函数满足如下性质。

①性质1：

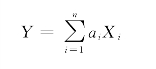
其中ai不全为0，则

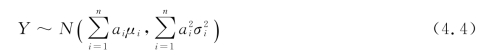
由于样本彼此之间独立且和总体的分布一致，而正态分布的随机变量之和仍然服从正态分布，因此样本的线性函数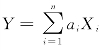仍然服从正态分布，而正态分布随机变量Y 的数学期望和方差可以通过概率论里数学期望和方差的性质求得。

②性质2：

这个结论是为了解决这样的问题：当总体服从正态分布时，样本均值也服从正态分布，甚至当总体是任意分布时，根据中心极限定理，在大样本的情况下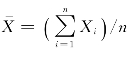，也近似服从正态分布，因此可查正态分布表来确定落在各个区间里的概率。

③性质3：

这个结论的用处是，通常都用S2来估计总体的方差σ2，而既然知道了就可以通过查χ2分布表，求σ2落在某些区域内的概率。

④性质4：

此结论的意义在于，当总体为正态总体N（μ，σ2）时，由于这样我们希望在用公式将其转换为标准正态分布后查标准正态分布表来求解概率问题，但在实际情况下，总体方差σ2经常是未知的，因此就可以利用这个定理，用样本方差S2来代替总体方差σ2，查t分布表来确定T 落在一些区域内的概率。

⑤性质5：

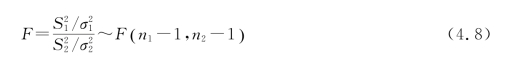
其中，是容量为n 1 的总体X 的样本方差，是容量为n2的总体Y 的样本方差。此结论的意义在于，当我们需要比较两个总体的方差时，此时无论是否已知两个总体的均值，都可以借助于这个定理计算样本方差、查F 分布表，从而确定上面的F 统计量落在一些区域内的概率。