8.1.2 定义
还是先以一元线性回归为例来讨论,对于一元线性回归式Y=β1+β2X+u 来说,X 也可以代表和Y 有非线性关系的其他模型,如在第7章中,如果得出Y 和ln Z 存在显著的线性相关关系,则也可以将其转化为线性模型Y=β1+β2ln Z+u 来求解。
一元线性回归的任务就是用恰当的方法估计出参数β1、β2,从而用样本回归函数Y=![]() 估计出总体回归函数,并且使估计出来的参数具有良好的统计特性。所以,从某种角度来看,回归问题也可以视为参数估计的问题。
估计出总体回归函数,并且使估计出来的参数具有良好的统计特性。所以,从某种角度来看,回归问题也可以视为参数估计的问题。
定义8.1 一元线性回归的总体回归函数有两种表现形式:条件期望表现形式、个别值表现形式。
(1)条件期望表现形式
当自变量X 取某一固定值时,Y 的取值并不确定,Y 的不同取值会形成一定的分布,这是Y 在X 取不同值时的条件分布。
![]()
(2)个别值表现形式
![]()
其中:(X1,Y1),(X2,Y2),…,(Xn,Yn)为样本对;n 为样本个数;ui为各个Yi与条件期望E(Yi|Xi)的偏差,显然ui是个可负可正的随机变量,代表排除在自变量Xi以外的所有因素对Yi的影响,称为随机误差项。
定义8.2 一元线性回归的样本回归函数为
![]()
其中,![]() 分别是β1、β2的估计值
分别是β1、β2的估计值![]() 为相应于Xi的计算值。
为相应于Xi的计算值。
样本回归函数中的参数![]() 与Y 的计算值
与Y 的计算值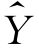 的关系,可用下面向量形式的公式表达:
的关系,可用下面向量形式的公式表达:
![]()
我们的任务是,求出这样的待估参数![]() 并且使估计出来的参数
并且使估计出来的参数![]() 具有良好的统计特性。
具有良好的统计特性。
求法一:普通最小二乘法。
使Y 与其计算值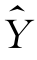 之间的“误差平方和”极小,设
之间的“误差平方和”极小,设![]() 也就是使
也就是使
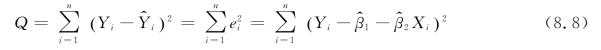
极小。为此,分别求Q 对![]() 的偏导,令其为0:
的偏导,令其为0:

就可以求出符合要求的待估参数![]() 这种估计系数的方法就称为普通最小二乘法。
这种估计系数的方法就称为普通最小二乘法。
如果是多元线性回归,则在模型Y=β1+β2X2+…+βkXk+u 中代入样本后,可得
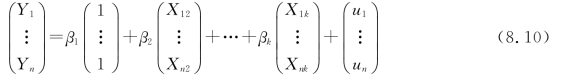
式(8.10)也可用向量、矩阵方式表达为
![]()
其中,X 是n×k阶矩阵。

则也可由普通最小二乘法求得![]() 使得
使得![]() 过程可参照式(8.8)和式(8.9),得出
过程可参照式(8.8)和式(8.9),得出
![]()
求法二:极大似然估计法。
4.2.2节中我们讲了极大似然估计法,假设在一次抽样中,样本X1,X2,…,Xn的取值为x1,x2,…,xn。在一元线性回归式Y=β1+β2X+u 的样本函数Yi=β1+β2Xi+ui中,高斯假设提出![]() ,因此,
,因此,![]() 即Yi的概率密度函数为
即Yi的概率密度函数为
![]()
极大似然估计法的原理:因为此时出现了样本观察值x1,x2,…,xn,这表明取到这一样本值的概率P{X1=x1,X2=x2,…,Xn=xn}比较大,我们当然不会考虑那些不能使样本x1,x2,…xn出现的![]() 作为β1、β2的估计。再者,如果已知当
作为β1、β2的估计。再者,如果已知当![]() 时P {X1=x1,X2=x2,…,Xn=xn}比较大,而其他β1、β2的估计值使P{X1=x1,X2=x2,…,Xn=xn}很小,我们自然认为取
时P {X1=x1,X2=x2,…,Xn=xn}比较大,而其他β1、β2的估计值使P{X1=x1,X2=x2,…,Xn=xn}很小,我们自然认为取![]() 作为β1、β2的估计值较为合理。
作为β1、β2的估计值较为合理。
极大似然估计法即取![]() 使
使
![]() (https://www.daowen.com)
(https://www.daowen.com)
其中L {x1,x2,…,xn;β1,β2}=P {X1=x1,X2=x2,…,Xn=xn}。
设总体X 是离散型总体,分布律为P {X=x}=p(x;β1,β2),则样本X1,X2,…,Xn取到x1,x2,…,xn的概率为
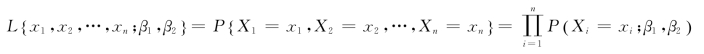
设总体X 是连续型总体,其概率密度为f(x;β1,β2),则样本X1,X2,…,Xn的联合密度为
![]()
则随机点(X1,X2,…,Xn)落在点(x1,x2,…,xn)的邻域(边长分别为d x1,d x2,…,d xn的n 维立方体)内的概率近似地为

其值随β1、β2的取值而变化,与离散型的情况一样,我们取β1、β2的估计值![]() 使概率式(8.17)取到最大值,但因子
使概率式(8.17)取到最大值,但因子![]() 不随β1、β2的取值而变化,故只需考虑函数
不随β1、β2的取值而变化,故只需考虑函数
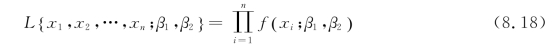
的最大值。所以
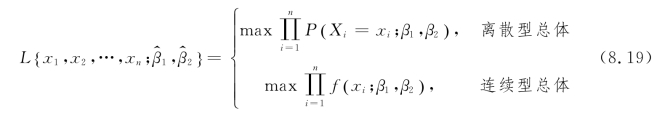
定义8.3 这样得到的![]() 与样本值x1,x2,…,xn有关,常记为
与样本值x1,x2,…,xn有关,常记为![]() (i=1,2),称为参数βi(i=1,2)的极大似然估计值,而相应的统计量
(i=1,2),称为参数βi(i=1,2)的极大似然估计值,而相应的统计量![]() (i=1,2)称为参数βi(i=1,2)的极大似然估计量。
(i=1,2)称为参数βi(i=1,2)的极大似然估计量。
我们再回到一元线性回归问题,此时
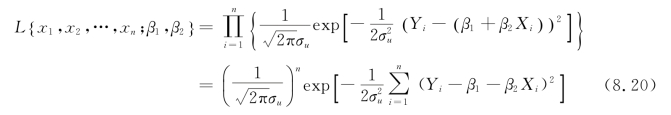
求max L {x1,x2,…,xn;β1,β2}等价于求![]() 使
使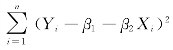 最小,这和普通最小二乘法求
最小,这和普通最小二乘法求![]() 的原理相同。所以,两种方法的结果是一样的。
的原理相同。所以,两种方法的结果是一样的。
按照上述两种方法,得出的计算公式如下:
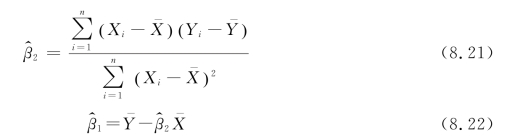
其中,![]()
利用样本观察值(x1,y1),(x2,y2),…,(xn,yn)得出![]() 后,下面可求出Y 的计算值向量
后,下面可求出Y 的计算值向量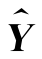 的值:
的值:
![]()
其中X 为样本向量,X=(X1,X2,…,Xn)T,xi为Xi(i=1,2,…,n)的样本观察值。而Y 的实际样本观察值yi并不完全等于Y 的样本计算值 ,在图形上看拟合后的直线和原样本对(x1,y1),(x2,y2),…,(xn,yn)生成的点状图在通常情况下并不是完全吻合的,如图8.2所示,图8.2中的空心点代表原样本对。
,在图形上看拟合后的直线和原样本对(x1,y1),(x2,y2),…,(xn,yn)生成的点状图在通常情况下并不是完全吻合的,如图8.2所示,图8.2中的空心点代表原样本对。
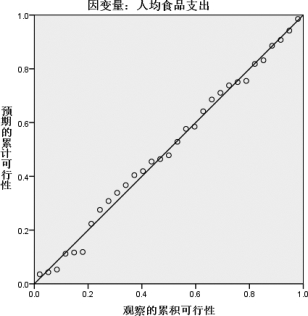
图8.2 一元线性回归拟合图
定义8.4 Y 的实际样本观察值与样本计算值之间会有一个偏差,这个偏差被定义为残差项、剩余项或残差向量,设为![]() 对于样本Y1,Y2,…,Yn来说,
对于样本Y1,Y2,…,Yn来说,
![]()
其中,![]() 见定义8.2,综合上面式(8.22)和式(8.23),可得
见定义8.2,综合上面式(8.22)和式(8.23),可得
![]()
其中,e=(e1,e2,…,en)称为残差向量,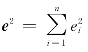 称为残差平方和,又记为Q。
称为残差平方和,又记为Q。
在例8.1中,有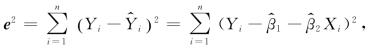 在估计参数β1、β2时,前面提到的两种方法都是取使得
在估计参数β1、β2时,前面提到的两种方法都是取使得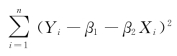 最小,得到估计参数
最小,得到估计参数![]() 即此时残差平方和e2也最小。
即此时残差平方和e2也最小。
注:![]() 是总体回归函数中参数β1、β2的估计,
是总体回归函数中参数β1、β2的估计,![]() 是对Y 的实际观测值Yi的估计,残差项ei在概念上类似于总体回归函数中的随机误差ui。
是对Y 的实际观测值Yi的估计,残差项ei在概念上类似于总体回归函数中的随机误差ui。
定义8.5 未解释方差![]() 的无偏估计
的无偏估计![]() 的定义如下:
的定义如下:

其中,k是包括常数项在内的解释变量数,对于一元线性回归来说,k=2。![]() 称为估计标准误差(SPSS 22中称为标准估算的错误)。
称为估计标准误差(SPSS 22中称为标准估算的错误)。
在证明回归系数的最小二乘估计法是最佳线性无偏估计时(本书证明略,证明可参见袁卫《统计学》的231页),讨论![]() 的方差除了涉及样本观测值以外,还涉及总体随机误差项ui的方差
的方差除了涉及样本观测值以外,还涉及总体随机误差项ui的方差![]() 由于ui不能直接观测,显然
由于ui不能直接观测,显然![]() 也是未知的,但是可以证明,在最小二乘估计法的基础上,我们可以得到
也是未知的,但是可以证明,在最小二乘估计法的基础上,我们可以得到![]()
