5.3.3　期望未知对正态总体方差的假设检验

5.3.3　期望未知对正态总体方差的假设检验

本节介绍本章开篇提到的情况三。

例5.6　某炼铁厂的铁水含碳量X 在正常情况下服从正态分布。现对操作工艺进行了某些改进，从中抽取5炉铁水，测得其含碳量数据如下：4.412、4.052、4.357、4.287、4.683，据此是否可以认为新工艺炼出的铁水含碳量的方差仍为0.1082（α=0.05）。

解：建立待检假设H0：σ2=0.1082；H1：σ2≠0.1082。在H0成立时，样本来自总体N（μ，0.1082）。这时

对于给定检验水平α=0.05，可用SPSS计算确定临界值如图5.9所示，使得

也可以选取参数k，使得

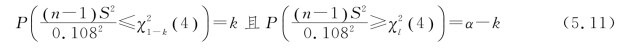
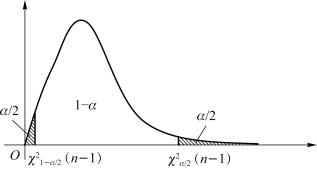
图5.9　例5.6的临界值法图示

将样本信息4.412、4.052、4.357、4.287、4.683代入式（3.10）（或在SPSS中通过单击【分析】→【描述统计】→【频率】计算）可以算出

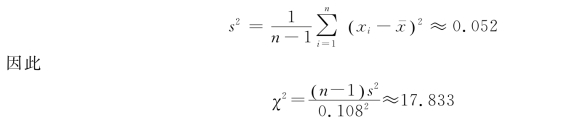
方法一：临界值法。

由SPSS查表求出因为

因此应拒绝H0，接收H1，即新工艺炼出的铁水含碳量的方差不能认为是0.1082。

方法二：p 值法。

由χ2=17.833，用SPSS（如图5.10所示）求出其右侧概率的2倍，并将其和检验水平α=0.05作比较。

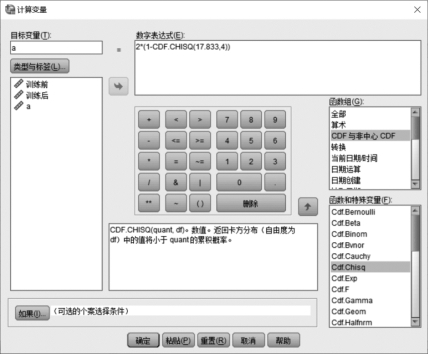
图5.10　计算统计值的p值

p 值为0.00266＜α=0.05，因此拒绝原假设H0，接收H1，即新工艺炼出的铁水含碳量的方差不能认为是0.1082。

课堂练习　分析例5.6中单尾检验的情况，即检验H0：σ2≤0.1082，H1：σ2＞0.1082，α=0.05。