6.3.1 有重复试验的双因素方差分析问题引入
为了理解双因素方差分析的基本思路,我们先举一个简单的例子。
例6.3 下面记录了3种教学方法分别在4 个不同学校3 个试验班的试验效果,如表6.14所示。
表6.14 有重复试验的双因素方差分析举例
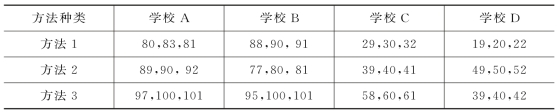
试分析学校、教学方法以及两者交互作用对试验结果的影响是否显著(α=0.05)?
1.双因素方差分析模块的SPSS操作示例
①读入数据(数据见文件“CH6例6.3教学法有重双因”)后,单击【分析】→【一般线性模型】→【单变量】,进入双因素方差分析模块。
②在双因素方差分析模块(如图6.10所示)中,选中左框的变量“试验结果”放入右边的“因变量”框中。
③选中左框的变量“方法”和“学校”,放入右边的“固定因子”框中,如图6.10所示。
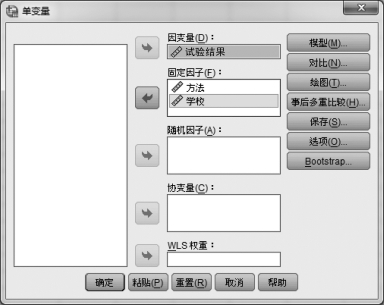
图6.10 双因素方差分析模块
④默认系统对双因素方差分析模块对话框右上侧【模型】的选择,即要做全分析,包括交互效应。
⑤单击【选项】按钮,系统弹出一个新对话框,如图6.11所示。在该对话框的上半部分,选择“OVERALL”,即对3个变量——方法、学校、方法*学校,都要做分析。在该对话框的下半部分,选择方差的“同质性检验”。
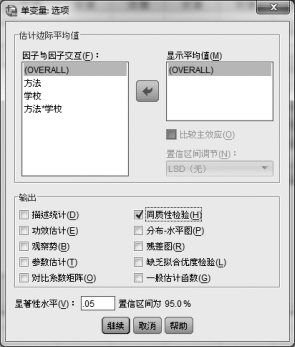
图6.11 “单变量:选项”对话框
⑥单击【继续】按钮,回到上一个对话框。
⑦单击【事后多重比较】按钮,系统弹出一个新对话框,如图6.12所示。在该对话框的上半部分,我们选择需要对因素的水平做两两比较的变量,这时该对话框下半部分靠上的“假定方差齐性”区块被激活,此时选择“LSD”,用最小显著性差异方法(t统计量的一种变形)来两两检验各水平效果均值是否有显著性差异。而该对话框下半部分的“未假定方差齐性”区块没有被激活,因为方差非齐性问题可以通过数据转换,使其接近齐性,如将Box-cox转换、对数转换、正态转换等转化为方差齐性来解决,所以SPSS在这个菜单下只针对方差齐性设计了算法。
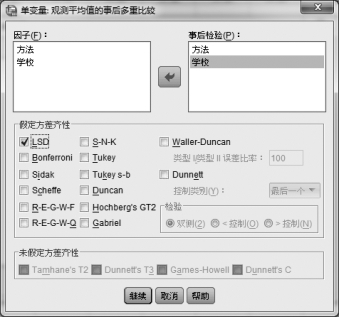
图6.12 “单变量:观测平均值的事后多重比较”对话框(https://www.daowen.com)
⑧单击【确定】按钮,输出结果,如表6.15~表6.18所示。
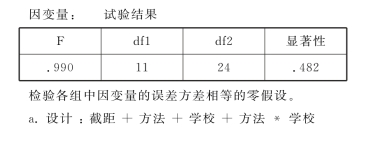
a.表6.15是方差齐性的检验结果,表中F 统计量的值为0.990,其显著性概率p=0.482>0.05,接受零假设,认为具有方差齐性。
表6.15 误差方差的齐性Levene's检验a
b.表6.16是含交叉项的双因素方差分析的结果。表中数据表明:
•方法作用的F 统计量的值为339.060,相应的显著性概率p=0.000<0.05,说明不同的方法对教学效果的作用是显著的;
•学校作用的F 统计量的值为2310.767,相应的显著性概率p=0.000<0.05,说明不同学校对教学效果的作用是显著的;
•方法与学校作用的交互作用的F 统计量的值为82.922,相应的显著性概率p=0.000<0.05,说明方法与学校作用的交互作用对教学效果的影响也是显著的;
c.表6.17是方法的不同等级对教学效果的影响的两两多重比较的检验结果,从显著性概率来看,3种方法彼此之间的显著性概率都小于0.05,所以方法的不同等级之间都存在显著性差异;
d.表6.18是学校的不同等级对教学效果的影响的两两多重比较的检验结果,从显著性概率来看,4个学校彼此之间的显著性概率也都小于0.05,所以学校的不同等级之间,除了学校A 和学校B 之间外,都存在显著性差异。
表6.16 主体间效应的检验
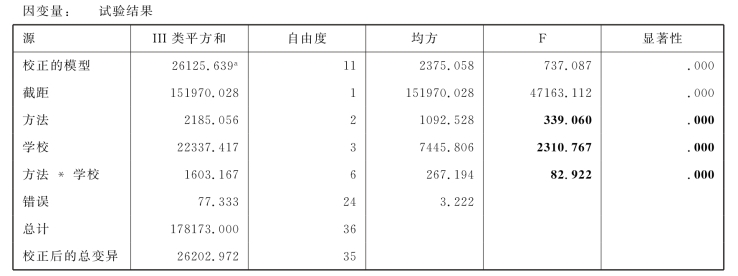
a.R 平方=.997(调整后的R 平方=.996)
表6.17 方法的不同等级的两两比较t检验
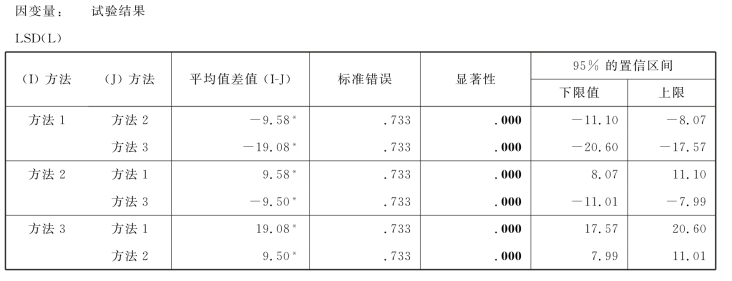
基于观察到的平均值。
误差项是均方(误差)=3.222。
*.均值差的显著性水平为.05。
表6.18 学校的不同等级的两两比较t检验
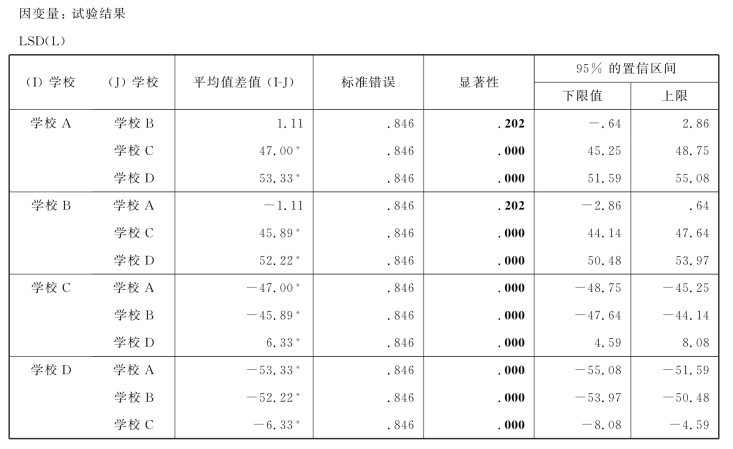
基于观察到的平均值。
误差项是均方(误差)=3.222。
*.均值差的显著性水平为.05。
