8.2.1 逐步回归问题引入
逐步回归法的基本思想：在考虑Y 对已知的一群变量X2，…，Xk回归时，从变量X2，…，Xk中，逐步选出对已解释变差的贡献（也就是偏解释变差，或称偏回归平方和）最大的变量，其将进入回归方程。而对已解释变差的贡献大小的判别依据就是包含了偏解释变差的F 统计量Fj。统计量Fj的最大值fj对应的xj先进入方程。最后一个进入方程的xj应当满足：其统计量的值fj的显著性概率p 小于或等于选定的显著性水平α（即要求其系数βj显著异于0）。这里需要提到一个新的概念——偏回归平方和，简单来说就是在模型已经含有其他自变量的基础上，加入一个新的自变量后，引起的对于回归模型贡献（回归平方和）的增加量，或者删除某个自变量后，引起的对于回归模型贡献的减少量。
反向逐步回归法指的是，先把Y 对所有的自变量X2，…，Xk回归，然后逐步把fj最小的xj剔除出方程。所有剔除出方程的xj在剔除时，其统计量的值fj的显著性概率p 大于选定的显著性水平α，即要求其系数βj 与0没有显著性差异。
例8.3 研究某城市散户股民的证券市场的“投入证券市场总资金”是否可以用变量“证券市场外的收入”“受教育程度”、“入市年份”和“股民年龄”来说明。数据见文件“CH8例8.3证券市场”。
①打开数据文件后，单击【分析】→【回归】→【线性】，系统弹出一个对话框。
②在该对话框的左栏中选择变量“投入证券市场总资金”，单击向右的箭头，将其放入“因变量”框中。在对话框左栏中选择变量“证券市场以外年收入”“受教育程度”“入市年份”和“年龄”（即股民年龄）单击向右的箭头，将其放入“自变量”框中，如图8.4（a）所示。
③单击“方法”对应的箭头，出现一个下拉菜单，有如下选择。
a.输入：让步骤②中选择的自变量全部进入模型中。
b.逐步：前向逐步回归法（逐步增加自变量）与后向逐步回归法（先把所有自变量放入方程，然后逐步减少自变量）结合的方法。
c.删除：在已有回归方程的基础上，根据所设定的条件，删除变量。
d.后退：先把所有自变量放入方程，然后逐步减少自变量。
e.前进：逐步增加自变量。
本例我们选择“逐步”，选择后如图8.4（b）所示。
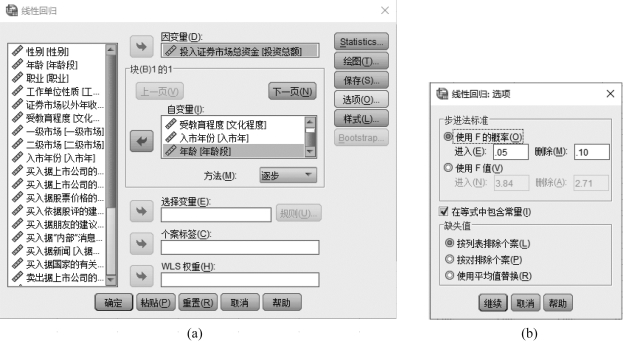
图8.4 多元逐步回归对话框
④单击“线性回归”对话框右下角的【选项】按钮，可以发现在上述3种逐步回归法（逐步、后退、前进）中，SPSS所默认的进入回归方程的变量的系数的F 统计量的概率为0.05，所默认的从回归方程中删除变量的系数的F 统计量的概率为0.10。两者的差距有明显的作用，它能够使进入回归方程的变量不容易从方程中剔除出去。在逐步回归的过程中，当新的解释变量进入方程后，一般会改变已经进入方程的贡献，使原来的Fj统计量的显著性概率发生变化，如变为0.08。如果从方程中删除自变量的显著性概率值还是0.05，那么这个变量Xj就应该从方程中剔除了。但是现在不用从方程中剔除这个变量Xj，因为0.08还小于设定的显著性概率值0.10。正因为如此，才避免了如下死循环的发生：一个解释变量Xj刚进方程→新的解释变量进方程后改变了Xj的Fj统计量的显著性概率，如变为0.08（大于0.05）→于是，Xj出方程→然后Xj又进方程→……。本例接受系统的默认值。单击【继续】，返回“线性回归”对话框。
⑤单击“线性回归”对话框右侧的【Statistics】按钮，弹出一个新的对话框，如图8.5所示。
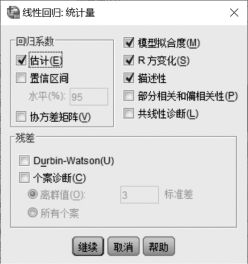
图8.5 “线性回归：统计量”对话框
a.在该“线性回归：统计量”对话框的“回归系数”区块中，有3项选择。
•估计：这是系统的默认值。选择此项后，系统会输出回归系数B、B 的标准差、标准系数贝塔、B 的t值及其双尾检验的p 值。
•置信区间：复选项。系统会输出每一个B（非标准化回归系数）的95%的置信区间。
•协方差矩阵：选择此项后，系统输出非标准化回归系数的协方差矩阵、各个变量之间的相关系数矩阵。
b.在“线性回归：统计量”窗口的右侧，有5个复选项。
•模型拟合度：这是系统的默认值。选择此项后，系统输出（在逐步回归的过程中）引入模型的变量、从模型中删除的变量、复相关系数R、判定系数R2、校正的R2、估计值的标准误差、ANQVA 方差分析表。
•R 方变化：在逐步回归中，当回归方程引入或删除一个变量后，R2会改变。选择此项，要求输出R2的改变量。如果
变化大，说明增加了这个变量，对模型回归效果的贡献大（或删除了这个变量，对已解释变差的影响小）。选择此项后，系统还将输出Fch、Sigch（做了变量增减后的F 统计量的p 值）。
•描述性：选择此项后，系统输出有效样本数、变量的均值、标准差、相关系数矩阵、单尾检验的显著性水平的p 值矩阵等。
•部分相关和偏相关性：选择此项后，系统会输出部分相关系数（一个自变量进入回归方程后，R2的增加量）、偏相关系数和零阶相关系数，这有助于对共线性的判断。
•共线性诊断：选择此项后，系统会输出有关多重共线性的诊断数值。
c.在“残差”区块中，有2个选项。
•Durbin-Watson：检验是否存在序列相关的统计量，输出检验序列相关的D-W 统计量的检验结果，本例在此不选此项。
•个案诊断：本例在此不选此项。如果选择此项后，以下两个子选项将被激活。第一个子选项为离群值：要求输入奇异数据的判据，默认值是大于或等于3倍标准差的为奇异值。第二个子选项为所有个案：系统会输出所有观察残差ei。
⑥单击【继续】按钮，回到“线性回归”对话框。
⑦单击“线性回归”对话框右上方的【绘图】按钮，系统弹出所要绘制图形的对话框，如图8.6所示。在该对话框的左框中有因变量和一些参数，可选一些变量或参数用箭头送入“X”（或“Y”）框，选其他参数送入“Y”（或“X”）框。完成计算后，系统就按照这里的选择输出图形。可供选择参数主要有如下几种。
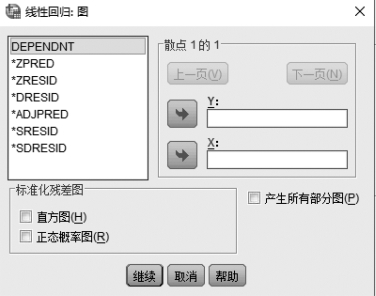
图8.6 “线性回归：图”对话框
•DEPENDNT：被解释变量，习惯上作为Y 轴，可观察被解释变量（就是模型中的Y）从小到大变化时，残差变化的情况（如观察是否存在非齐次方差，是否存在序列相关等）。
•ZPRED：标准化预测值，习惯上也作为X 轴，可观察被解释变量标准化后的计算值（就是模型中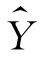
）从小到大变化时，残差变化的情况（如观察是否存在非齐次方差，是否存在序列相关等）。
•ZRESID：标准化残差，习惯上作为Y 轴，可观察它随被解释变量（或被解释变量标准化的计算值）变化的情况。以下的各类残差项在习惯上多作为Y 轴，可观察它们随被解释变量增大时的变化情况。
•DRESID：剔除残差。
•ADJPRED：修正后的预测值。
•SRESID：t分析残差。
•SDRESID：t分析剔除残差。
⑧单击【继续】按钮，返回“线性回归”对话框。
⑨在“线性回归”对话框中，单击【保存】按钮，可将有关计算结果保存下来。
⑩单击【确定】按钮，系统输出结果。
下面对结果进行分析。我们只解释其中的两类表：方差分析表（表8.10）与系数表（表8.11、表8.12）。
表8.10的第一列给出了逐步回归过程中的4个模型。从中可以看到，平方和（“平方和”列与每个模型的“回归”行的交叉位置上的数据）随着逐步回归的过程，不断增大：从43 028.424增大到54 693.770。这就是说，随着逐步回归中模型的改进，已解释变差越来越大。从表8.10中的最后一列可以看到模型b和c的F 统计值的显著性概率都小于0.01，说明两个模型的总体回归效果都是显著的。
表8.10 回归问题中的方差分析表
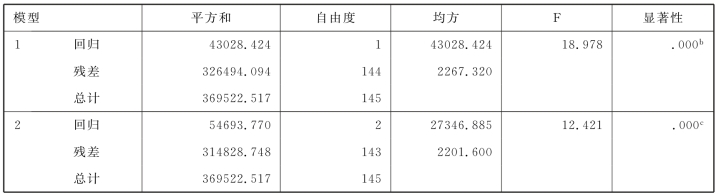
a.因变量：投入证券市场总资金
b.预测变量：（常量），证券市场以外年收入
c.预测变量：（常量），证券市场以外年收入，年龄
表8.11的第一列是对模型的解释变量的说明；第二列为回归系数非标准化的回归系数
“标准误差”为
的标准误差
第三列为标准系数贝塔；第四列为t值；第五列为t值的显著性概率p 值。
“受教育程度”和“入市年份”没有进入方程，从所有模型的所有解释变量的t检验情况来看，假设显著性水平为0.05，变量“证券市场以外年收入”“年龄”在0.05的水平上，均显著异于0。而常量的显著性概率0.508＞0.05，所以建议读取表8.11中“标准系数贝塔”列的结果。“证券市场以外年收入”“年龄”可以作为解释变量存在于模型中，解释投资额的变化。
表8.11 回归系数与显著性检验表a
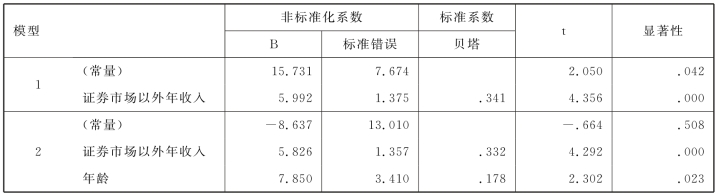
a.因变量：投入证券市场总资金
表8.12是排除的系数的显著性检验表，“受教育程度”和“入市年份”没有进入方程，从表中可以看到这两个变量以及常量的系数显著性概率的变化情况。
表8.12 排除的系数的显著性检验表a
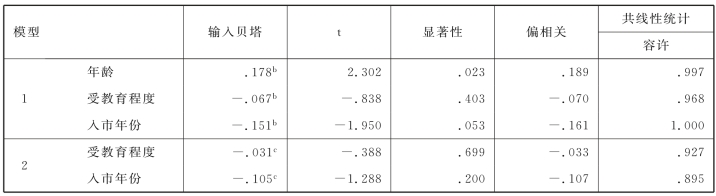
a.因变量：投入证券市场总资金
b.模型中的预测变量：（常量），证券市场以外年收入
c.模型中的预测变量：（常量），证券市场以外年收入，年龄