3.4.3 表示刻度级数据的茎叶图、直方图
在上面介绍的饼图和条形图中,已经看不到数值了,因此很难从图形恢复数据的原貌。那么,还有什么图形方法可以更好地展示数据特征?我们来看下面这个例子。
例3.10 某班男生的身高数据(单位为cm)(对应数据文件“CH3例3.10直方茎叶箱”)如下:

请绘制直方图与茎叶图。
1.SPSS操作示例
①在录入数据(或打开数据文件“CH3例3.10直方茎叶箱”)后,单击【分析】→【描述统计】→【探索】,用箭头将“身高”变量送入“因变量列表”框中。此时系统对话框如图3.20所示。在图3.20中,左下角的“输出”区块的默认值“两者都”的含义是同时输出统计量和图形,本例选择接受它。探索模块对话框右上角的【Statistics】按钮中的默认值是输出95%的置信区间,这以后再详细介绍。
图3.20 探索模块对话框
②单击【绘图】按钮,系统默认值是输出箱形图和茎叶图。本例接受这个默认值,并且在直方图的复选框处也打钩,如图3.21所示。
图3.21 “探索:图”对话框
③单击【继续】按钮回到探索模块对话框,然后单击【确定】按钮。系统输出统计结果和统计图,图3.22和图3.23是该样本数据集合的直方图和茎叶图的图形统计结果。
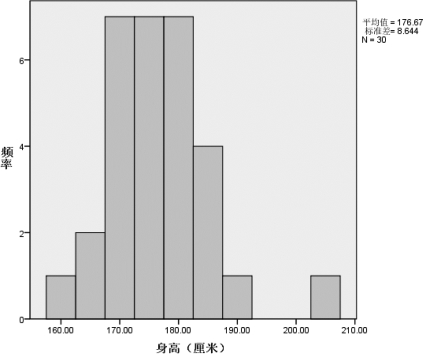
图3.22 男生身高数据的直方图

图3.23 男生身高数据的茎叶图
还可以选择【图形】→【旧对话框】→【条形图】,也可以生成相应的条形图,如图3.24所示。
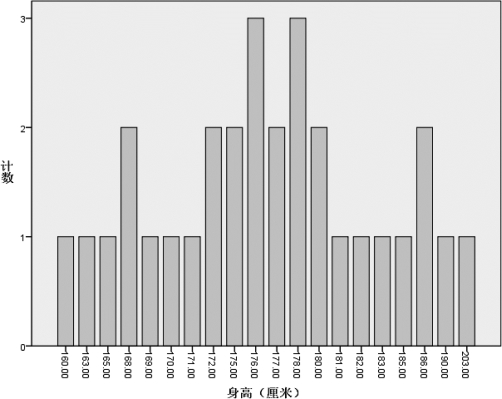
图3.24 男生身高数据的条形图
2.直方图与茎叶图的概念解析
1)直方图
条形图用矩形条的高度来表示横坐标相应位置上样本值出现的频数或频率,能够形象地展示样本数据集合的数据结构。但它也有一个弱点:对于刻度级的数据而言,当数据的精度(相对)高,使得不重复的数据非常多或使得重复数据相对少(即同一数据的频数或频率小)时,人们反而看不清数据集合的结构。例3.10的条形图(如图3.24所示)就反映出了条形图的弱点。
因此,需要一种类似的,但却适用于大量不重复样本值的图示方法,这就是直方图图示法。直方图是定量变量最常用的图表示方法之一。例3.10的直方图如图3.22所示,其做法是,把横轴分成若干区间(通常是等宽度的区间),然后计算数据在各个区间上的频数(频数),并在各区间上画出高度与数据在相应区间的频数成比例的矩形条。纵坐标当然也可以是频率,即把频数除以样本量,这并不改变图的形状,而仅仅使纵坐标单位不同。
直方图的初步概念可以从如下直方图的基本做法中反映出来:①按照样本值的大小,选择恰当的区间长度(通常要求区间是等长度的),对所有的样本值分组;②统计所有组(区间)内的样本值个数(频数),或各个组内的样本值个数占全部样本值总个数的比例(频率);③用横坐标按照顺序表示不同的区间(组),用竖立于区间上的矩形条高度表示相应区间的样本值的频数或频率。这就是直方图。
不难看出,直方图与条形图的本质差异在于:直方图要对数据进行分组(或者说按照一定刻度范围把相邻的数据并为一组);而条形图不对数据分组,直接统计不同样本值的重复次数(或者也可以理解为只把相同的数据作为一组)。
这就是说,只要区间足够小,使得每个不重复的样本值处于不同的区间中,这时的直方图就是条形图。也就是说,可以把条形图看作直方图的特例。
不考虑特殊情形,由于直方图要按照合适的区间(一般是等长的区间)对数据进行分组,因此,它只适用于刻度级的样本数据(不论是刻度级数据中的定比级数据还是定距级数据,都可以)。(https://www.daowen.com)
当然,如果有特殊需要(如定序级数的不重复数据太多),也可以“强行”把相邻的定序级的数据划为一组,然后按组来统计频数与频率。但这时的组不是区间的概念,也不存在“等长”的组的概念,仅仅是集合的概念。
2)茎叶图
首先,我们来看一下茎叶图的基本概念与适用范围。
茎叶图适用于刻度级(定比级和定距级)数据,但不适用于定类级数据,勉强适用于定序级数据,不过提供不了比条形图更多的信息。例3.10的茎叶图如图3.23所示。
以例3.10中的男生身高数据为例,它既展示了身高的分布形状又有原始数据,它仿佛一片带有茎的叶子,茎为较大位数的数字,叶为较小位数的数字。可以看出,图3.24是用代码打印出来的若干行数目,所以不像真正意义上的图形。SPSS软件输出的茎叶图前两行说明,小数点相应于茎叶界限的位置。对于图3.24,小数点位于符号“&”下方所代表的一列。这个茎叶图中茎的单位为10,叶子单位为1。在数据的第一行指出了一个身高为16×10+0=160cm和16×10+3=163厘米的2个身高数据,第一列Frequency对应的数值2即表示数据第一行的这两个数据。而数据第3行的茎为17,因此叶子中的3个数字0122代表3个身高数据170cm、171cm、172cm、172cm。最后一行展示的1个身高为190cm。
显然,茎叶图既表示了原始数据,也有直方图显示数据分布的特点。但是茎叶图也有弱点,即当数据量很大(比如有成千上万个度量)时,茎叶图就无法显示了。这也是这里只用了30个男生的身高数据,而没有把全校所有男生的身高数据都录入做茎叶图的原因。
另外,也可以把几个茎叶图画在一起进行对比。比如,两个不同总体如果含有同样的变量,那么这两个总体关于该变量的数据可以共用一个茎,“背靠背”地展示叶子,用来形象地进行比较。茎叶图并不“漂亮”,不懂的人不一定能够马上理解,因此在媒介中很少出现,“茎叶图”显然是前计算机或早期计算机时代的产物。
(1)适用范围
茎叶图适用于顺序级以上的数据。
(2)基本含义
按照某个一致的规则,把所有的样本值分成“茎节”和“叶”两个部分。“茎节”在左,“叶”在右。“茎节”“叶”之间用小数点隔开。
如果对某个样本数据集合规定,所有样本值的百位数为“茎节”(这时称“茎节”的宽度为100),所有十位数和个位数为“叶”,这样,样本数据123的“茎节”就是1,“叶”就是23。“茎节.叶”的表达方式就是1.23(应当同时注明“茎节”的宽度为100)。这样,我们就很容易从“茎节.叶”表达方式的1.23,推出该样本值是123。
当然,也可以规定所有的百位数和十位数为“茎节”(此时称“茎节”的宽度为10,意思是“茎节”末位上的数字1表示10),所有的个位数为“叶”,这样,样本数据123的“茎节”就是12,“叶”就是3,“茎节·叶”的表达方式是12.3(应当同时注明“茎节”的宽度为10)。
(3)“茎节”的宽度
确定“茎节”宽度的原则:“茎节”要有变化。
样本值=“茎节.叶”表达ד茎节”的宽度
(4)“茎节”的长度
“茎节”的长度=允许的最大叶值-最小叶值+1
如图3.24所示,因为下方标注了“Stem width:10.00”,即“茎节”的宽度为10,因此16.0表示的样本值是160。
把样本数据集合中的所有不相同的“茎节”,按照从小到大的顺序连接起来,就构成了这个样本数据集合的“茎”,显然“茎节”的宽度就是“茎”的宽度。
例3.11 打开数据文件“CH3例3.8 统计学成绩50”,得到下面图3.25所示的茎叶图,问:①Stem width:10是什么意思?②共显示了多少个数据?③列出头3个数据。
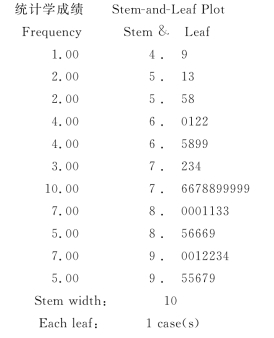
图3.25 统计学成绩数据的茎叶图
解:①Stem width:10的含义是“茎节”的宽度是10,即每一个显示的数据的实际样本值大小为显示值的10倍。
②共显示了1+2+2+4+4+3+10+7+5+7+5=50个数据。
③头3个数据是49、51、53。
