4.3.2 区间估计的理论分析
用点估计来估计总体参数，即使是无偏、有效的估计量，也会由于样本的随机性，从一个样本算得估计量的值偏离所要估计的参数真值。而且，即使二者真正相等，由于参数值本身是未知的，因此也无从肯定这种相等。到底二者相差多少？这个问题换一种提法就是，根据估计量的分布，在一定的可靠程度下，指出被估计的总体参数所在的可能数值范围。这就是参数的区间估计问题。
区间估计的具体做法是，找两个统计量
使
其中，0＜α＜1，α一般取0.05或0.01，则称随机区间
为β的100（1-α）%的置信区间。百分数100（1-α）%称为置信度或置信水平。
1.正态总体均值μ的区间估计
（1）方差已知，对总体均值进行区间估计
例4.5 假设某节能灯灯泡的寿命服从正态分布N（μ，8），从中抽取了10个节能灯灯泡进行寿命试验，得到的数据（单位为小时）如下：1050、1100、1080、1120、1200、1250、1040、1130、1300、1200，试找出平均寿命区间（α=0.05）。
解：设样本（X1，X2，…，Xn）来自正态总体N（μ，σ2），则
选取含有已知变量最多的统计量来对未知参数进行区间估计，由于正态总体的方差已知，则根据式（4.5），查表可求得zα/2，使得
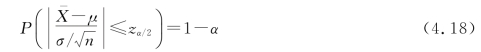
观察式（4.18），我们可以通过左侧括号中的运算，求得μ的一个置信区间。那么这里变量zα/2是未知的，怎样查表求得zα/2？zα/2的下角标α/2有什么含义？
在式（4.18）左侧中，为了求得μ的区间范围，交换绝对值运算中分子上两项的位置
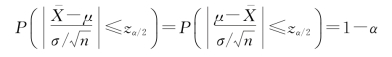
展开绝对值，整理得
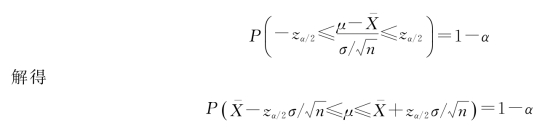
那么，
就是总体均值μ的置信区间，而这里的zα/2是未知的。在概率统计的命名规则中，在一般情况下以临界值右侧的概率作为该临界值的下角标，如图4.8所示，服从标准正态分布的随机变量
的概率密度函数是关于y轴对称的，又因为
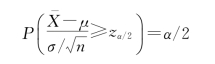
所以，这里用zα/2来标记临界值点。
zα/2的求法可以通过查标准正态分布的概率分布表获得，还可以用SPSS求得，后者是本书中所用的方法，下面会对其进行介绍。由图4.8可见，标准正态分布的分布函数在zα/2的值为
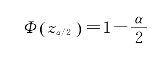
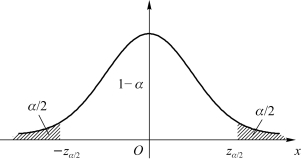
图4.8 zα/2求解示意图
因此μ的置信度为1-α的置信区间是
在这里，只有zα/2是未知的，怎么求zα/2？zα/2由公式
查表可获得。在本例中α=0.05，可查表求得zα/2=1.96（若α=0.01，可查表求得zα/2=2.58）。又由n=10，σ=2.8284，可算出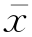
=1147，则进一步计算可得
即μ的置信区间为（1145.25，1148.75）。
（2）用SPSS从x查p=P（X≤x）和从p查x
下面我们来看怎样由已知概率1-α/2用SPSS求临界值zα/2，以及怎样由zα/2求概率值。
任意打开一个数据文件，在数据视图窗口中，单击【转换】→【计算变量】，系统弹出“计算变量”对话框，如图4.9所示。在这个对话框的右边，有一个“函数组”框，在这个框中有很多函数组，从中选出你所需要的函数组，完成相应的计算。例如，可以从随机变量X的取值边界x，计算出概率值p。也可以反过来，从概率值p，计算出x的值。这样，就免去了查表的麻烦。
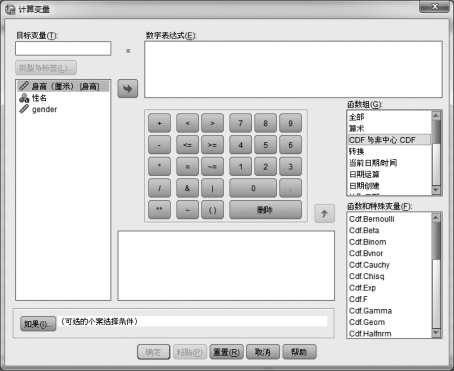
图4.9 在“计算变量”对话框右侧选择“函数组”
例如，要计算服从N（0，1）分布的x=1.96的概率值P（X≤1.96），就在图4.9所示的对话框中的“函数组”框中，选中函数组“CDF 与非中心CDF”（累积密度函数）。此时，该对话框右下方的“函数与特殊变量”框中就会出现大量的可供选择的累积概率密度函数，如图4.9所示。
在这个“函数与特殊变量”框中选择“Cdf.Normal”函数，这时，这个框左侧的框中出现对这个函数的解释。用向上的箭头把这个函数送到上面的“数字表达式”框中。此时，“数字表达式”框中，出现函数CDF.NORMAL（？，？，？），这两步操作的结果如图4.10所示。
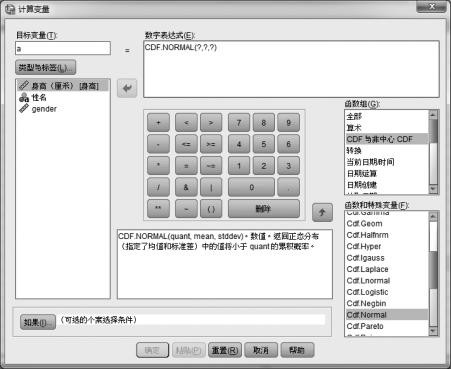
图4.10 在“计算变量”对话框右下框选择函数
按照图4.10中的文字解释，在“数字表达式”框中把函数CDF.NORMAL（？，？，？）的第一个问号改为1.96（即x 的值），第二个问号改为0（即标准正态分布的均值），第三个问号改为1（标准正态分布的标准差），即将CDF.NORMAL（？，？，？）改为CDF.NORMAL（1.96，0，1）。
在图4.10左上角的“目标变量”框中，输入你希望的变量名，如a、b、aa等。本例输入a，单击【确定】按钮，数据视图窗口中就出现变量a的值是0.975，也就是P（X≤1.96）=0.975。
从概率值反求x 的操作方法类似上述过程。
例如，假设X 服从N（0，1）分布，已知概率值P（X≤x）=0.975，要计算x 的值，就可以按类似于上述的过程操作。在刚才的“计算变量”对话框中，单击【重置】按钮，清空刚才的操作。然后，在图4.9所示对话框的“函数组”框中，选中函数组“逆DF”。
此时，该对话框右下方的“函数和特殊变量”框中出现大量的可供选择的反概率密度函数。选中正态分布的反函数“Idf.Normal”，并用向上的箭头把这个函数送到上面的“数字表达式”框中。并把该框中的函数IDF.NORMAL（？，？，？）改为IDF.NORMAL（0.975，0，1）。然后，在图4.10左上角的“目标变量”框中，输入你希望的变量名，如b、ab等，本例输入b。单击【确定】按钮。数据视图窗口中就出现变量b的值是1.96。
同样，也可以计算其他分布函数（如t分布）的概率值和反函数的概率值。这样可以省去查表的工作了。
（3）方差未知，对总体均值进行区间估计
例4.6 假定初生婴儿（男孩）的体重服从正态分布，随机抽取12名婴儿，测得其体重分别（单位为g）为3100、2520、3000、3000、3600、3160、3560、3320、2880、2600、3400、2540。试以95%的置信水平估计新生男婴儿的平均体重区间。
解：设样本
来自正态总体
，由于σ2未知，且
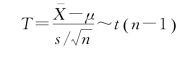
查表可求得tα/2（n-1），使得
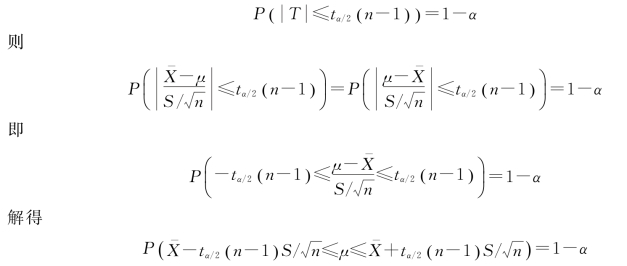
所以，在这道例题中，设新生男婴儿体重为X，由于X 服从正态分布，方差σ2未知，因此借助于t分布。对于a=0.05，因样本数n=12，则用上面讲过的SPSS求值法，或者查自由度为11的t分布表，得tα/2（11）=2.201。再计算
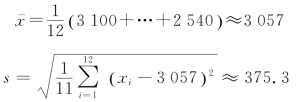
因此，新生男婴儿的平均体重μ的95%的置信区间为
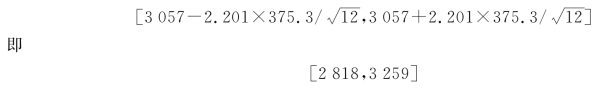
例4.7 结合4.3.1节讲的SPSS操作的例4.4，再从公式计算的角度分析，根据随机选取出来的32场报告会的听众人数数据，估计覆盖全校500场报告会的平均听众人数的95%的置信区间。数据文件见“CH4 例4.1报告会”。
解：设32场报告会听众人数的数据，即样本（X1，X2，…，Xn），来自正态总体
由于σ2未知，则利用
可求出置信区间。其中样本观察值可由表4.3读出，
可利用SPSS求出，即单击【转换】→【计算变量】→【逆DF】→【IDF.T（0.975，31）】，得出tα/2（31）≈2.04，将其代入区间的计算公式，四舍五入，保留两位小数，可得
这样，我们从理论计算和SPSS软件操作两方面都能求出置信区间了。
（4）一般总体大样本下总体均值的区间估计
根据中心极限定理，对于不是正态分布的一般总体，当样本容量相当大时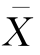
渐近地服从正态分布，故在大样本情况下，对于一般总体仍可用正态总体的办法对总体均值进行较精确的区间估计。
在n=30时，就可把总体看作近似服从正态分布
，当然n越大越好。
2.未知总体均值，正态总体方差σ2的区间估计
例4.8 假定初生男婴儿的体重服从正态分布，随机抽取12名婴儿，测得其体重（单位为g）分别为3100、2520、3000、3000、3600、3160、3560、3320、2880、2600、3400、2540，对婴儿体重的方差进行区间估计（a=0.05）。
解：设样本（X1，X2，…，Xn）来自正态总体N（μ，σ2），此例中，服从正态分布的婴儿的体重均值μ未知。由4.1.3节知
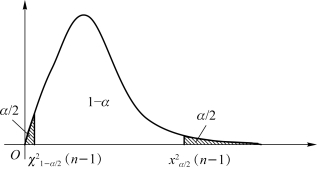
图4.11 χ2（n）分布区间估计求解示意图