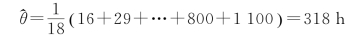4.2.2 点估计与判断点估计的优劣标准
1.点估计的概念
设待估计的参数为θ，如总体分布中的均值、方差等，现在从总体中得到一个随机样本X1，X2，…，Xn，如何根据样本信息估计θ？
记估计θ的统计量为
，它是关于样本X1，X2，…，Xn的函数，简记为
我们称
为θ的估计量。
若得到一组样本观察值x1，x2，…，xn，就可以得出θ的估计值
总体分布参数θ的点估计就是求出θ 的估计值
2.统计量的优劣标准
由样本观察值出发，利用点估计的方法可以获得若干个θ的估计值，那么哪个估计值更好一些？这就需要用一些恰当的标准来判别。
（1）无偏估计
根据样本推得的估计值与真值可能不同，然而，如果由一系列抽样构成各个估计，很合理地会要求这些估计的期望值与未知参数的真值相等，它的直观意义是样本估计值在未知参数的真值周围摆动，而无系统误差。
定义4.1 如果
成立，则称估计值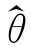
为参数θ 的无偏估计。
例4.2 从总体X 中抽取样本X1，X2，…，Xn，E（X）=μ，D（X）=σ2。试证明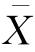
及S2分别是μ及δ2的无偏估计量。
证明：由数学期望和方差的性质，可以证得
是μ的无偏估计量。而
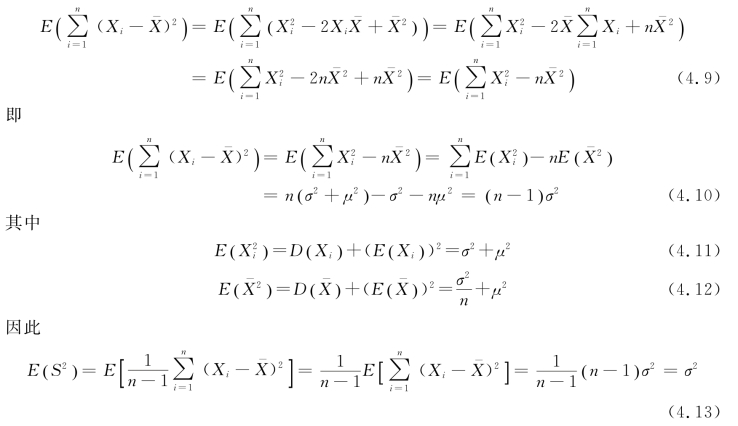
所以，S2为σ2的无偏估计。
（2）有效估计
定义4.2 设
都是θ的无偏估计，若它们的样本容量均为n，而
的方差小于
的方差，则称
有效的估计量。
（3）一致估计
在一般情况下，统计量
但希望当n→∞时，
这就是说，希望当样本容量n无限增大时，估计值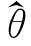
在真值附近的概率趋近于1。
定义4.3 如果当n→∞时，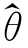
依概率收敛于θ，即对任意给定的
则称统计量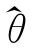
为参数θ的一致估计。
3.获得点估计量的极大似然估计法
根据从总体X 中抽到的样本X1，X2，…，Xn，对总体分布中的未知参数θ进行估计。极大似然估计法是要选取这样的值，当它作为θ的估计值时，使观察结果出现的可能性最大。在一般情况下，可以利用极大似然估计法估计离散型总体的概率函数中的参数θ，和连续型总体的概率密度函数中的参数θ。
定义4.4 设X 为离散型随机变量，有概率函数
为待估参数，则似然函数
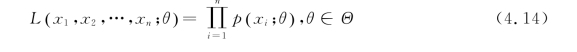
对每一取定的常数样本值x1，x2，…，xn，L 是参数θ 的函数，则称L 为样本的似然函数（如果θ是一个向量，则L 是多元函数）。
定义4.5 设X 的概率密度是f（x，θ），其中θ是未知参数，可以是一个值，也可以是一个向量，由于样本的独立性，则样本x1，x2，…，xn的联合概率密度函数是
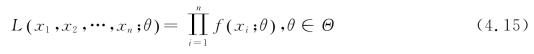
定义4.6 如果L（x1，x2，…，xn；θ）在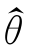
处达到最大值，则
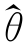是θ 的极大似然估计值。
由R.A.费希尔（R.A.Fisher）引进的极大似然法的原理是：对于出现的样本观察值x1，x2，…，xn，在θ取值的可能范围Θ 内挑选使似然函数L（x1，x2，…，xn；θ）达到最大的参数值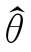
，将其作为参数θ的估计值。极大似然估计值
与样本有关，是样本的函数。由于ln L（x1，x2，…，xn；θ）与L（x1，x2，…，xn；θ）同时达到最大值，所以为了计算方便，只求ln L（x1，x2，…，xn；θ）的最大值。即计算
解出θ的估计值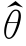
。
如果待估计的参数θ 是一个向量，即θ=（θ1，θ2，…，θm），则解如下的方程组，求出
例4.3 某电子管的使用寿命（从开始使用到初次失效为止）服从指数分布，其概率密度函数如下：
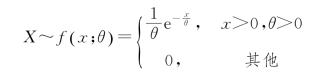
x1，x2，…，xn为X的一组样本观察值，今抽取一组样本，其具体数据（单位为h）如下：16、29、50、68、100、130、140、270、280、340、410、450、520、620、190、210、800、1100。问如何求θ的极大似然估计值？
解：似然函数
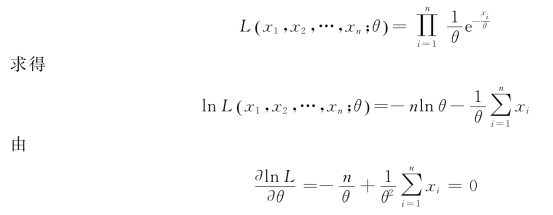
解得
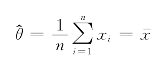
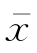就是θ的极大似然估计。因此参数θ的估计值为
