正弦波的重要性
迄今为止我们只谈到了声波的两个特性元素,即振幅和波长。也就是说,我们还未谈及声波的具体形状,即波形(waveform)。
对于像音叉这样的简单声源而言,音叉的齿像钟摆一样上下振荡,这样一个周期产生的波形就是正弦波(sine wave)。比音叉更复杂的声源所发出的波也比正弦波更为复杂,这是因为这类声源发出声音时的运动也更复杂。例如,小提琴在演奏一个音符时的过程就是一个典型的例子。小提琴的弦进行着复杂的运动,其中一些弦向着一个方向振动。与此同时,另外的一些临近的弦正在向着相反的方向振动,这两部分弦的振动方式都相当复杂。公元1801年,一位法国数学家金·伯提斯·傅立叶(Jean Baptiste Fourier)曾经有一个重大的理论突破。他发现像振动的小提琴琴弦这样复杂的声源,可以被分解成许许多多基本的成分,而当这些成分被加在一起时,又可以重新描述琴弦振动的整体过程。傅立叶发现所有复杂的运动,包括声音在内,都可以被分解成多个正弦波。
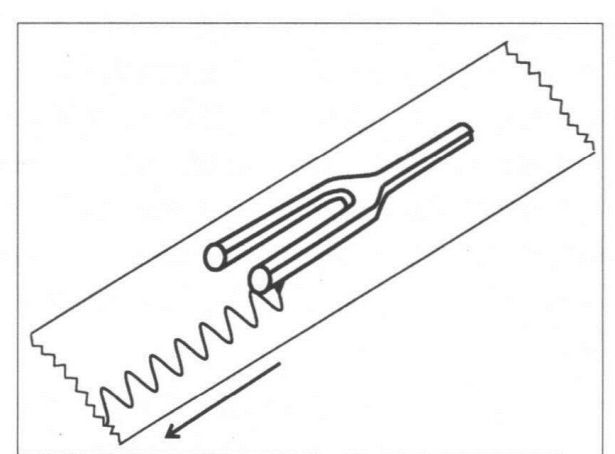
图1.8 随着时间的推移,音叉的一个齿的运动轨迹描绘出了一个正弦波形。波的形状与时间的比值我们称其为“波形”。
当小提琴家一个音符接着一个音符地演奏时,小提琴声波的波形在迅速地变化着。有时即便是在一个音符当中,颤音[2]的使用也会使波形产生很大变化。不过通过对每个旋律点的频率分析(frequency analysis)〔也叫频谱分析(spectrum analysis)〕,可以使我们了解到这个音符是由哪些正弦波组合成的,而这些正弦波又是如何组成复杂的复合波形的。傅立叶还发现,不仅包含着许多正弦波的复杂波形是以一种特殊的方式——谐波方式在彼此之间产生着紧密联系的,连许多正弦波之间也是如此。这表明任何波形都可以被分解成基音(fundamental frequency)和一系列的谐波(harmonic)。谐波以基音(fundamental)的两倍、三倍甚至更多倍的形式存在,例如,当小提琴在演奏小字一组的“a”时,基频为440Hz,同时,它的谐波分别为880Hz、1320Hz以及1760Hz等等。
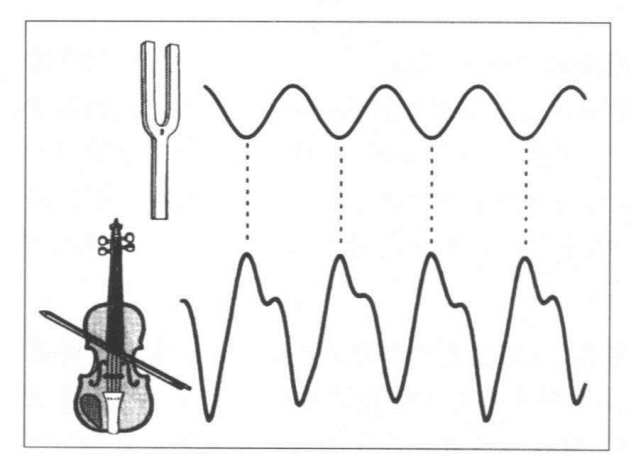
图1.9 音叉的振动发出了正弦波,而小提琴的琴弦更为复杂的振动则发出了更为复杂的波形。究其原因,主要是较复杂的振动在基频的基础上加入了谐波的成分。
如果想更好地理解这些复杂的振动是如何发生的,可以参考一把吉他的琴弦的振动过程。吉他琴弦的两端被固定在琴板上,人们通过拨弄弦的中间使其发声。它的基频(基波的频率)与琴弦在一次运动中上下移动的总长度是对应的。同时,声波的振幅在弦中间时的最大值到弦末端弦夹处几乎无振幅的最小值之间不断地发生变化。
琴弦还可以同时以谐频(谐波的频率)振动。例如,相对于基频而言,如果把琴弦的一半频率进行提升,另一半进行衰减,当琴弦再次发出这一谐波时,就好像琴弦的两端被夹紧了一样。这时的谐频与基频极其相近,同时听上去又有夹住弦的中部的感觉。这时的谐波以两倍基频的频率方式传播,主要是因为被分别处理的两段琴弦在各自独立地振动,其中每段琴弦都以两倍基频的频率振动。这就叫作二次谐波(the second harmonic)。
不要因为这个谐波是在基波之后出现的第一个谐波,而将其误称为“一次谐波”。要记住虽然事实如此,但我们仍称其为“二次谐波”。
上述过程在基频的三倍频率、四倍频率及多倍频率时都会发生,从而形成了多次谐波。一根琴弦在同一时间里可以多种方式进行振动,即同时以基频和谐频的方式振动,这样形成的是一种复杂的振动。此时,组成复杂振动的各种方式很难彼此分辨出来。在振动描绘出的曲线上,任意地抽出一点都可以说是基频与谐频的叠加。
在识别不同的声源时,一个重要的方法就是通过识别声源发出的不同谐波来辨别声源。不同的乐器在演奏同一音高时,其音色的不同主要是通过谐波成分的不同而体现出来的。比如,小提琴的谐波构成的范围就不是非常广,它的谐波强度也不像小号那样大。正因如此,小号的音色听起来就比小提琴要明亮(brighter)。将小号的频谱分析与小提琴的频谱分析进行比较,可以明显看出小号的谐波成分比小提琴要延展许多,在力度上也强许多。
谐波的另一种叫法是“泛音”(overtone、partial)。上述谐波定义虽然相对简单易懂,但真实乐器的原理却远比这些要复杂得多。它们在传播基频和谐频以外的其它频率波时,其过程也是一样的。
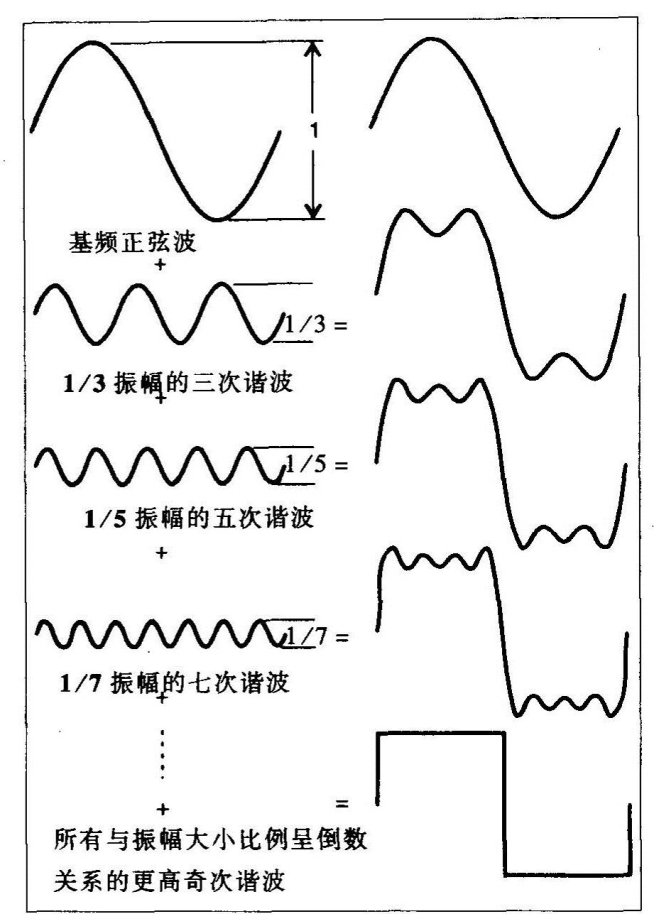
图1.10 像方波这样较为复杂的波是由多次谐波组成的——方波包含了三次谐波(3rd harmonic),其振幅为基波的1/3,以及五次谐波(5rd harmonic),其振幅为基波的1/5等等。
目前,由乐器演奏出的一些有音调的谐波发声原理,我们已经比较清楚了。那么,那些音调不是很清晰的声音,比如像在海边听到的人的谈话声和海浪声等等又会是怎样的呢?这些声音有谐波吗?虽然构成不是很明显,但“海边低声谈话”的这类声音也是由基波和谐波组成的。同时,基波和谐波变化得也非常之快。如果想找到海边谈话声的基频,要比找到歌声的基频困难多了(如果音高很准,那么只要从频谱分析中就可以找到其基频了)。但即便如此,海边谈话声的基频还是可以找到的。
声学家通常把基频非常明显的声音定义为乐音(tonal),而把那些基频不是很明显的声音定义为类噪声(noise-like)。噪声(noise)有许多种定义,其中最为普遍的一种是指人们不愿听到的一种不受欢迎的声音。声学家认为海浪的声音是一种接近噪声的声音,因为,海浪声的基频很难准确地找到,除非海浪声在某些特殊时刻对某些人而言是悦耳的或是刺耳的,但这就需要依靠人们的主观感受而定了。像海浪这样的噪声在同一时间里会产生许多正弦曲线频率(sinusodal frequency)。把这些频率分成基频和谐频的困难在于,当人们无论用专业设备还是用人耳对其进行分辨时,这么多同时出现的频率并无明显的排列次序。关于基频和谐波的讨论还可以延伸到“次谐波”(sub-harmonic)领域。有些设备和乐器所发出的波的频率,往往是基频的1.5倍或1.25倍等。对于乐器而言,这种频率可以给乐器的音色加上一种“厚重”的感觉。
