直观想象的解读
![]()
在《义务教育数学课程标准(2011年版)》中,有两个概念:空间观念和几何直观。显然,“直观想象”是整合了“空间观念”和“几何直观”两个概念,而空间观念就是空间想象,指具体事物和几何图形之间的互译;几何直观主要指用图形描述和分析数学问题,体现的主要是数形结合思想。
案例 两个代数公式的几何模型,如图1.1、图1.2。
完全平方公式 a2+2ab+b2=(a+b)2
平方差公式 a2-b2=(a+b)(a-b)
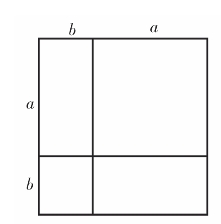
图1.1
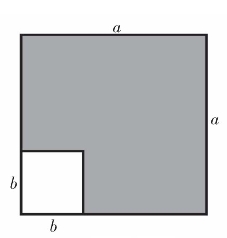
图1.2
案例 a2-b2与(a-b)2的区别,可用图1.3解释。
教学发现,学生经常出现(a-b)2=a2-b2,如果一味要求学生死记硬背公式,始终有部分学生把a2-b2与(a-b)2两个式子混淆。如果我们采用图形描述的方法,让学生从直观上分析,就会有效避免出现错误。
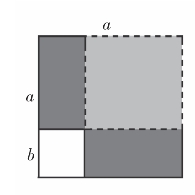
图1.3(https://www.daowen.com)
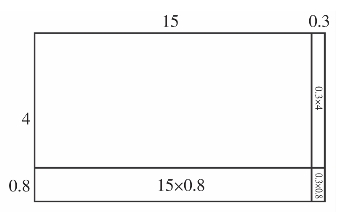
图1.4
再如,一道计算题目的错误解答,可用图1.4解读。
15.3×4.8
=15×4+0.3×0.8
=60+0.24
=60.24
![]()
数学学习离不开直观想象。因为数学本身就是研究数与形的学科,而直观想象不仅与“形”有关,也与“数和形”之间的关系也有关。
首先,直观想象的训练,能够培养学生数学的应用意识和能力。数学建模中的许多问题都与直观想象相关,因为我们的现实世界是直观的、形象的、三维的,数学建模往往要依附直观想象,通过对图形的数量抽象建立模型。
其次,直观想象的训练,可以提高学生的数学化归能力。将复杂问题化为简单问题、不熟悉的问题转化为熟悉的问题、未知化为已知,等等。特别是数与形之间的转化是一种典型的化归方法。如,在研究函数的性质时,我们总是通过画出函数的图像,而后结合图像去探究函数的性质,这种“数形结合”的思想方法贯穿整个函数学习的过程。不仅函数的学习如此,所有数学问题的解决,当我们的思考遇到障碍时,都可以借助图形辅助解决,所以直观想象是一种非常重要的数学素养。
再次,直观想象训练,也可以培养学生思维的深刻性和灵活性。我们观察几何图形,往往需要抽象出其隐藏的数量关系,分析隐含的几何模型,这些都是数学抽象过程,需要深度思考。另外,图形问题的解决方法经常具有多样性,如辅助线的添加方法不止一种时,如何选择最优方法,就体现了对思维灵活性的培养。
