凸显素养立意,建构“生长”课堂
杜威指出:教育即生长。生长是教育的目标,引导学生在课堂中不断成长是教育工作者的重要使命。初中数学教学要以“促进学生生长”为中心,创设合适的思维场景,顺势而为,建构数学生长课堂。引导学生主动探究、深度思考,培养理性思维,发展数学核心素养。
![]()
生命的本质特征是自然生长、必然生长。数学教学的价值在于思维教学,思维教学的关键在于创设思维必然的场景,从而让学生通过数学活动学会数学思维,提升数学核心素养。当下的数学课堂“重教轻学”的现状普遍存在,学生的数学学习仍处在被动状态。教师的教学视野依然停留在“如何有效让学生接受知识是这样的”,而没有关注“如何让学生思考知识是怎样生长成这样的”。教学设计过多地注重充分有效的预设,而忽视了自然灵动的生成。鲁教版初中数学八年级“平行四边形”有这样一道题目:
现有一块平行四边形的花坛,计划种植两种不同的花卉,要求两种花卉的种植面积相等,每块的形状不限。请你设计一下划分方案,画出图形并说明理由。
这个问题的解决,很多教师习惯先给学生提供几种图形,要求对照图形说明面积相等的理由。这样处理就使学生局限在老师预设的方案中,并且思维产生了依赖,学生就不会去主动思考探索属于自己的思路与方法,从某种意义上讲,仍然是老师牵着学生的鼻子走。如果教师能够大胆放手,给学生提供“留白”问题情境,课堂就会收获不一样的精彩。下面是笔者在给学生充分的时间去探究后,呈现的问题解决过程:
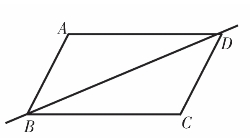
学生首先想到的是连接对角线,将平行四边形分割成两个全等的三角形(如图4.1和4.2),这是最简单最基础的几何构图。
 (https://www.daowen.com)
(https://www.daowen.com)
图4.1
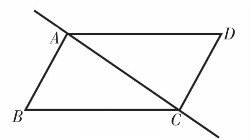
图4.2
还有一部分学生想到了分割成两个平行四边形,即过一组对边的中点作直线(如图4.3和4.4),此时也可以将原平行四边形分割成面积相等的两部分。理由不难解释,可以用平移的方法,将其中一部分沿着AD(或BC)方向平移AD的距离,则两个部分可以完全重合,说明两个小四边形的面积相等。
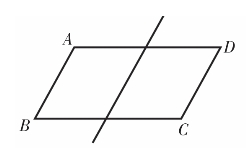
图4.3
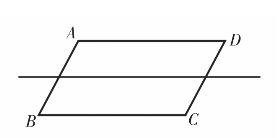
图4.4
教师继续提问:刚才的分割线都有特殊性,要么过顶点,要么过中点,你觉得还有没有其他的方法呢?启发学生继续思考,进入第二轮探究。
经过合作探究,学生经过尝试后又发现:如果这条直线截一组对边,所得的两个交点能够满足到各自顶点的距离相等(如图4.5和4.6中的AE=BF),此时分得的两个小四边形的面积也是相等的。理由:一是直接证明,利用梯形的面积公式,上底、下底和高分别对应相等,因此两个梯形的面积相等;二是间接证明。有个别学生会联系图4.1和4.2,受到这两个图形的启发,想到连接对角线,将两个梯形分割成三角形,对应的每一对三角形构成了八字形的全等,由此可得两个梯形的面积相等。实际上,第二种方法也为后面归纳出分割线所具有的共性(过对角线交点)埋下了伏笔。
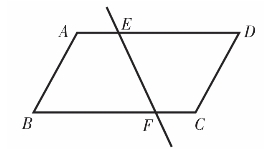
图4.5
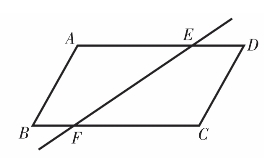
图4.6
此时,教师追问,前面这么多的方法,所画出的分割线是否具有共同特征呢?于是学生又投入到新一轮的深度思考。
当学生把先前几种方法的分割线都汇集到同一个图形中(如图4.7),马上获得了令人激动的发现:这些分割线都交于一点,而这个交点就是平行四边形两条对角线的交点,即平行四边形的对称中心。此时,为什么前面各种方法都可以满足分得的两部分面积相等就有了统一的理由:因为平行四边形具有中心对称性,当我们把平行四边形绕着对角线的交点旋转180°,分割成的两个图形的各组对应顶点重合,也就是说分得的两个部分重合,所以其面积相等。由此我们就得到了一个一般性的结论:一个平行四边形,当分割线过对角线的交点(对称中心)时,所分得的两部分图形面积一定相等。
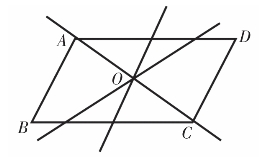
图4.7
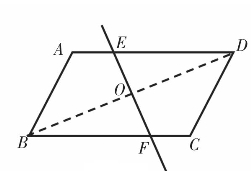
图4.8
最后,学生对照图4.8写出具体的推理过程,梳理巩固并再次体验前面发现的规律。
![]()
拥有生长力量的课堂是我们共同的追求。关注学生的生长,要给予他们生长的机会。这就要求教师在教学时,不仅要赋予课堂以生命力,还要研究如何立足教材和学生的数学现实,开发课本习题的潜在价值,以问题生长的形式挖掘教材习题深层的本义,为学生的数学学习搭建再创造的资源,让学生在解决问题的过程中,提高数学学习力。
![]()
思维方式,决定学习的效率。学习最大的差别,就是思维方式的差别。如果思维模式过于单一,思考的深度和广度都不够,导致思维过于片面。学生的认知学习,正如一场“盲人摸象”。如果总是从一个角度去看待问题,那就无异于故事里的盲人。可是,如果我们具备多元思维,就能把知识有机地结合起来,并贯穿在一个系统的思维框架中,就如同我们从多个角度去摸大象,把整个大象都摸一遍,那么我们就能无限接近大象的样子,透过现象看到本质,从而更好地解决问题。查理·芒格的多元思维指出:我们手中不能只有一个锤子,而需要拥有一个工具箱。在课堂教学中,引导学生从多个角度去分析解决同一道问题,既注重通性通法又倡导一题多解,将解题策略与方法内化于心。
促进学生数学思维生长,不能一蹴而成,而要将其贯穿在教学的全过程中。教师要注重灵活处理教材,科学应对课堂生成,关注学生的感受和反馈,并依据学情不断改进思维场景和教学活动,让学生思维自然地生长,从“想得到”到“想得妙”,最后伸展到“想得透”。教育的价值在于促进学生内在成长。将生命成长理念迁移到数学教学活动之中,找准学生数学素养生成的起点,还原数学素养生成的情境,让学生学习有生长力的数学,助力学生生命成长,这也是数学生长课堂的意义所在。
