动静有致，打造“真实”课堂
新课改以来，评价一堂课精彩与否，大多指向课堂的“动态性”活动。“动”的教学方式可以使学生保持积极的思维状态，使沉闷、静止的课堂气氛变得活跃、生动。但就目前的课堂教学而言，在向“动态式”的方向发展中，产生了很多的误区。重“动”轻“静”，以“动”代“静”；片面追求热闹，把以“生”为本搞成了以“声”为本；课堂已经偏离了课改的初衷，忽略了教育本真。学习是一个自我修养、静静思考的过程，课堂需要“静”的回归。
大容量、快节奏的课堂是很多教师心目中的好课。课堂上每个环节衔接紧凑，感觉学生不停地在思考，貌似学习一直在发生。可是每当进行教学评价时，很多学生并没有达成既定目标，甚至个别学生一无所获。究其原因，就在于学生缺乏深入思考的“静”界。教师为了完成既定的计划，只顾匆匆赶着学生向前跑。学生虽然始终在紧张的状态中，但却只是被动运转的机器。
片段一：教师出示题目后，不等学生充分思考，便抽生回答，最终课堂变成了极少数优生的舞台，其余学生云里雾里不知所云……
片段二：学生做书面练习时，教师边巡视边提醒：同学们要抓紧时间！已经有三分之一的同学做完了，其他同学快点啦！……看似营造了你追我赶的竞争氛围，实际上剥夺了学生静思的空间。
片段三：教师出示问题后，学生一时没有思路，课堂气氛“沉闷”，教师马上组织小组讨论，课堂气氛立刻“活跃”了起来，问题也很快得以解决。小组汇报时的发言往往只浮于表面，没有深入到问题的实质。因为教师没有创设一种宁静的氛围，学生缺乏独立深入的思考，导致解答停留于浅表。
教学中不能搞题海战术，教师要放慢脚步，让学生有静思的机会。课堂上，不时给学生很安静的几分钟……口动有声、心动无痕，真正有效的思维活动，往往是“无声”的内化过程。“静”并不等于思维的静止，而是一种别样的生动。
经常会看到这样的现象：学生的回答不尽如人意时，教师马上改变提问对象，让其他学生帮忙补充，此时最初那个学生的思维瓶颈就被教师的“救助”掩盖了！学生机械地跟着教师的节奏走，至于为什么非要如此，自己原本的路为什么走不通，心中并不明了。因而，当他再次遇见这类问题时，往往又会回到最初的思路上。于是教师们纷纷感慨：为什么反复讲过的题型，学生就是做不对呢？学生的听讲真是令人失望……其实根本原因是，教师没有给学生质疑顿悟的时间。
格式塔学习理论认为，学习的过程不是尝试错误的过程，而是顿悟的过程，由顿悟而掌握的学习有利于适应新的情境，解决新的问题。当学生对问题认识模糊不清时，学习就处于“顿”（停顿）的阶段，此时教师要做的是帮助学生自己来解决问题。首先，对于学生的大胆设想给予充分肯定，对其合理成分及时给予鼓励。然后对其失误及时因势利导，通过设置有创意的教学活动，激发学生质疑反思，找到解决问题的途径与方法。之后还要鼓励学生归纳总结，认识问题的本质，实现由“顿”上升到“悟”。绘制学科思维导图，是顿悟学习的最佳手段之一。在完成思维导图时，学生需要静心思考，准确提炼关键词，标示知识间的逻辑关系，并进行推理演绎。这个过程有助于提高学生结构化思考问题的能力。还学生质疑顿悟的“静”界，助其养成良好的思维习惯，而这个好习惯足可以决定命运，改变人生。
一直以来，数学课堂倡导问题引领教学。教师课前做充分预设，设置问题链，将问题分解得细致入微，学生一路高歌直达彼岸，课堂看似充满了生命活力。但若静下心来观课，会发现仍然是教师主宰着课堂，学生的思维没有生长的空间。当学生遇到新情境时，就会出现束手无策的表现，无法独立分析问题、解决问题。数学课堂上，教师一定要舍得放手，懂得退位，把探究知识的主动权交给学生，即使学习之旅走得磕磕绊绊，但他们会在困难中成长思维，在困惑中收获经验。
如，加减法解二元一次方程组。教师出示下面四个题目，让学生先自主尝试求解。
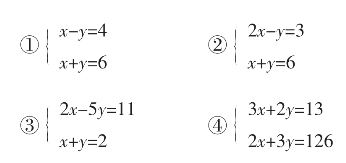
方程组①学生首先利用前一节课学习的代入消元法求出解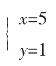
教师引导学生观察代入后的方程2y=2（或2x=10），实际上可以利用等式的基本性质，将两个方程的左右两边分别对应相加（减）即可实现消元，得到一个一元一次方程，从而求得解。这样就自然引入新知的学习：加减消元法解二元一次方程组。
继续解决②③④。如果在传统的教学中，教师会领着学生一起分析，引向教材中的系数扩大倍数法。而当我们把问题全部抛给学生自主去探索，学生就会呈现意想不到的思维成果。
学生A：方程组②我是这样求解的。类比方程组①，我想把两个方程直接相加消去y，得到关于x的一元一次方程，先求出x，再代入方程组中任意一个方程（当然选择第二个方程计算更为简便）即可求出y值。
学生B：方程组②的解法还可以消去x。我发现两个方程中未知数x的系数成2倍关系，因此可以利用除法将其系数变成相等的值。具体的就是，将第一个方程两边同时除以2，得方程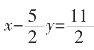
，然后将所得的这个新方程与第二个方程相减，即可消去未知数x，从而得到关于y的一元一次方程，实现了消元的目的，进一步解出方程组。
学生C：我认为A、B两个同学的方法都正确，因为他们都是通过乘除系数，使方程组中某一个未知数的系数相等（或互为相反数），再通过两个方程相减（加）达到消元的目的。相比而言，A同学的方法计算比较简便，而B同学的方法则是将方程组②转化为方程组①的特征，体现了由一般到特殊的数学思想方法，这种方法也非常有价值。
此时，教师作适时评价指导：A、B两位同学都非常善于动脑，能够自己独立分析问题并找到了解决问题的方法，值得大家为之点赞！C同学的交流也非常全面到位，解二元一次方程组时，要观察方程组中两个未知数的系数具有怎样的特征，思考我们应如何运用乘除（倍分）的方法进行消元。带着你的收获继续完成第③个。
学生D：方程组④我尝试分别用A、B两位同学的方法求解。对比发现，如果将方程两边同时除以某个未知数的系数时，所得新方程的系数都是分数，计算比较麻烦，不如用扩大倍数法将某一个未知数的系数变成相等或相反数。因此，我建议今后我们在用加减法解二元一次方程组时，尽可能用倍数法。而且尽量选择系数之间是整数倍的系数消元，进行简便运算。整个探究过程，教师悄然退位，静静聆听生命拔节生长的声音……宁静的课堂，生动的思考，充盈着外静而内动的美！
有人说，教学中的动静之道，就像花儿与绿叶，静是绿叶能量的积蓄，动是花儿精彩的绽放。课堂教学是个动态的过程，就真实的课堂而言，应该是动静有致。合理处理好教学中静和动的关系，才能创造出理想和谐的课堂教学。毕竟，有了“静”的厚积，才会有“动”的薄发。还学生一片“静”界，课堂才会更加真实生“动”！