课堂观察的有效实施
课堂观察不同于传统的听评课活动,它需要观察者、被观察者、学生三个对象合作,完成整个观察活动。由于课堂涉及的因素很多,我们需要建立一个简明科学的观察框架作为观察的抓手,避免课堂观察的随意和散乱。课堂观察框架可以分为四个维度:学生学习、教师教学、课程性质和课堂文化。这个四维框架的使用具体表现为以下几个问题:(1)学生在课堂中是如何学习的?学习是否有效?(2)教师是怎么教的?教学行为是否适当?(3)本节课的学科性表现在哪里?(4)“我”对这节课的整体感受是怎样的?这些问题可以借助具体可操作的观察工具——观察量表来进行记录和分析。
观察维度:教师教学
研究问题:问题设计与学习目标达成的关联度
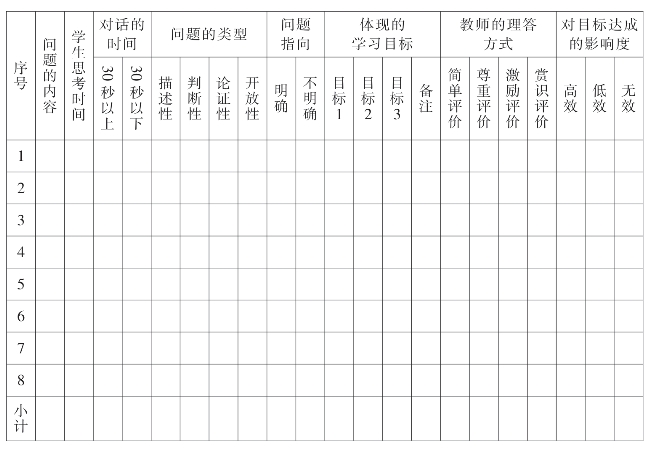
观察维度:学生学习·达成
研究问题:学生对核心知识的理解和运用怎样?
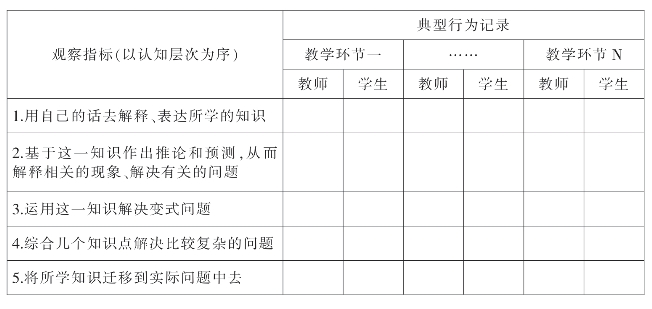
观察维度:课堂文化·思考(https://www.daowen.com)
研究问题:怎样以问题引领思考?
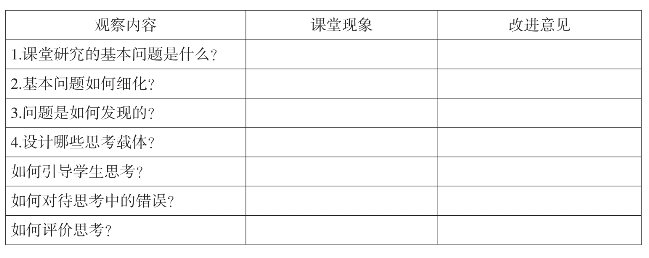
观察维度:课程性质
研究问题:如何更好地发挥教学目标对教学活动的引领作用?
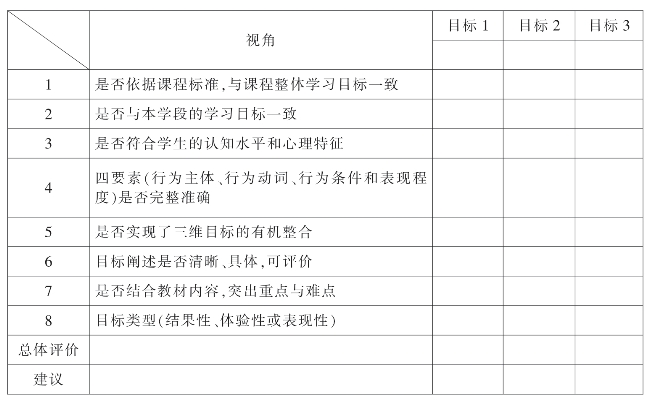
案例《解直角三角形》
教师A
观察维度:教师教学 观察点:教师提问与目标达成
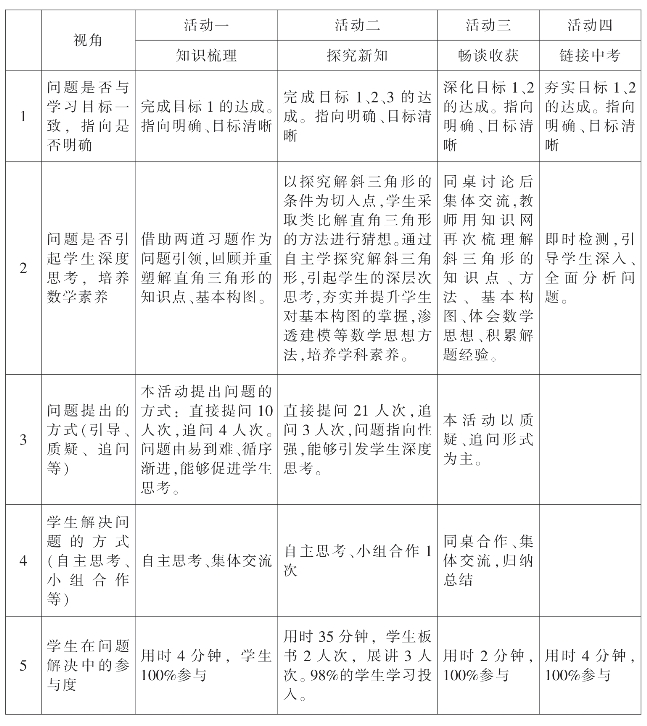
观课报告:
1.设计精心、知识系统。本节课从学生已有的学情出发,利用两道简单的题组作为问题引领,4分钟的自主学习回顾解直角三角形的条件、方法,这个低起点的引入既面向了全体学生又启发了学生学习的欲望。紧接着通过环节二探究新知,本环节教师设置的这几个问题引发了学生的思考,然后通过画一画、添加适当的条件,让学生在此过程中感知由特殊到一般、类比转化,以及方程等数学思想,同时感受数学的严谨性,强化了几何基本构图,将学生的解斜三角形的思路引到深处,促进学生的深层思考。从而将解斜三角形的知识点串成线,连成片,结成网。
重视建模、凸显过程。在环节二教师巧妙地设置问题,在学生的最近发展区设置问题,借助这个知识的“生长点”,引发了学生的深度思考,让学生在自主探究的过程中感受到了基本构图的重要性,通过画图感知、通过自主学习让学生再次建立基本构图的意识。学生在这个过程中发现、感悟、理解、运用,发展高阶思维。本节课中教师与学生在互动时关注的不是结果而是知识的生成过程。例如于老师不断的追问学生“你是如何得到的?说说你的理由。”学生在环节二的活动中,不仅完成了巩固练习,更重要的是感知了解斜三角形的思路、方法、技巧,提升了几何直观意识。
多种学习方式,突出学生主体地位。本节课教师通过设置问题串,引导学生自主探究,眼、手、脑并用,学生的主体地位得到了充分的体现。夯实基础的同时又发展思学生的创新维,培养了学生数学学科素养,使有限的课堂变成了全员参与、人人思考的无限空间。
教师B:
观察维度:教师教学 观察点:问题情境与深度学习
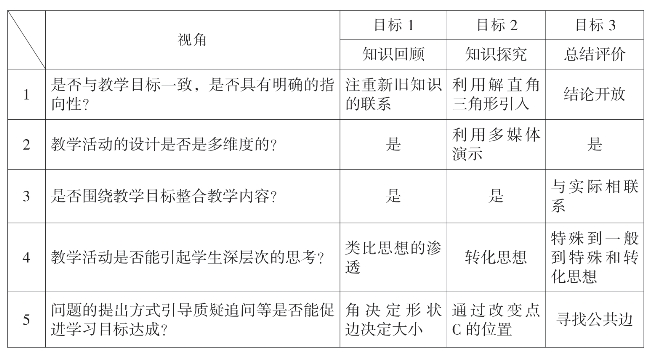
续表
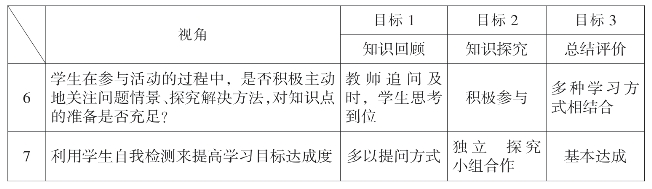
教师B的观课报告:
本节课赵老师依据学情进行教学设计,教学目标明确,环节清晰,采取设问、追问形式调动学生的学习兴趣和积极性,学生思维活跃,主动思考。教师引导学生运用化归思想把斜三角形转化为直角三角形,把不熟悉的问题转化为熟悉的问题,让学生很容易接受。师生互动,生生互动,合作探究,不断尝试,知识、能力水平都得到了提高。针对上面的观察量表说一下这节课的具体情况。
1.亮点
问题驱动,引领深度学习。本节课赵老师总共提问34人次,学生扮演7次,小组讨论两次,在知识的回顾中用时5分钟,探究一12分钟,其中跟踪练习4分钟,探究二15分钟,探究三8分钟,跟踪练习用时3分钟,总结1分钟,时间安排合理有效。问题是所有学习行为的源头,本节课教师将问题贯穿于整个教学活动,并通过不断追问引导学生学习新知识和提升数学思维。比如再可以添加什么条件?通过这个环节你有哪些收获?是不是所有的钝角三角形都是这样的解题思路?特殊角可以解斜三角形,那么一般的角是不是也能解呢?等等这些问题的提出都能促进学生的深度思考与学习,而且从学生回答来看,学生面对老师的问题积极性很高,这说明学生对知识能够积极建构,有很好的倾听和自主学习的习惯。教师能够在需要深入思考的问题、推理性的问题、创造性的问题,以及需要对知识进行归纳的问题上及时提问追问,大大的锻炼了本班学生学习习惯和提升数学思维能力,归纳能力。
重视数学思想方法教学及学习方法的培养。整个教学过程中让学生充分体会了由特殊到一般再到特殊,转化等数学思想方法的应用。教师在每一组类型题后都让学生回顾,总结提升,有利于学生加深对于具体数学知识的理解与掌握,从而达到迁移应用的目的。
课堂组织形式多样化,有利于本节课学习目标的达成。教师或让学生独立思考,或让小组讨论,学生口头回答或上黑板前讲,这些学习形式都利于学习目标达成效率的提高。
2.建议解直角三角形和解斜三角形都需要的是三个条件,不能让学生认为直角三角形需要两个条件,应该强调只要给的条件满足三角形全等的条件就行。
教师C:
观察维度:课程性质 观察点:即时评价
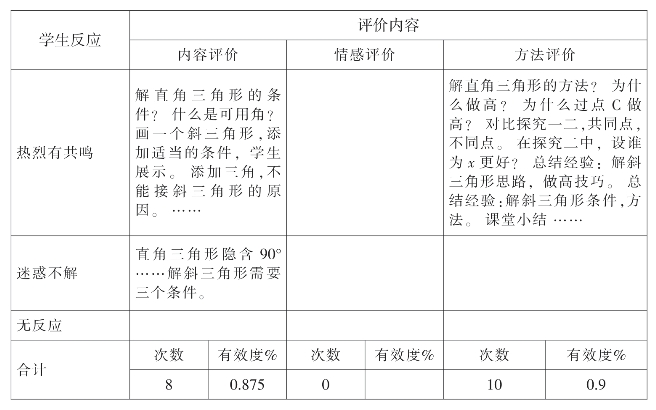
观课报告:
1.定量分析
这节课于老师通过学生自主探究、教师引导提问驱动学生思考,评价层次清楚,时间安排合理。根据统计,在知识梳理的环节,即时评价4次,在探究环节,共评价了16次,在课堂小结的环节,共评价了两次。从数据看,主要是内容性的评价和方法性的评价,其中内容性的评价有8次,方法性的评价有10次。教师的即时评价主要在探究新知中,评价精炼有效,对学生的反馈、追问、纠错、点评都及时有效。
于老师的问题紧紧围绕教学目标进行设计,多数评价指向明确,有效的引领学生思考。对于老师的提问,学生的参与度比较高。在学生回答问题之后,老师及时评价,如:非常好,还有没其他方法?这种方法更简单。通过追问引导学生深层次思考,归纳总结方法,积累丰富的活动经验。
2.定性评价
本节课是一节成功的新授课。首先回顾解直角三角形需要哪些知识?为本节课的学习打好基础。接着猜想解斜三角形需要几个条件,然后让学生自主探究:画一个斜三角形,添适当条件。然后分别探究两角即一角对边,两角及夹边两种情况。
于老师的课是一节开放性的课堂,整节课以学生探究为主,教师引导为辅。于老师一开始利用两道习题回顾解直角三角形的条件,用类比猜想的数学方法,为学生探究解直角三角形的条件,打下了良好的技术储备。学生通过两角一边,两边一角,三边,三角为分类讨论,自主发现三角解不出三角形。学生的大思路清晰,发散性思维得到了极大提升。
在具体探究两角一边类型时,学生通过自主探究、小组讨论、黑板展讲的方式,总结出来解题方法,例如化斜为直、过不可用角做垂直这两种方法,老师总结分析得很透彻。
本节课教师注重变式训练,有两边及其一边的对角变换为两边及其夹角,由锐角三角形变为钝角三角形,由已知边可直接用变为不可用,需要设未知数,丰富了题型,扩展了学生思维。
教师重视解题技巧,数学思想方法的总结提升。在每个探究之后都设置分享经验,引导学生思考:解斜三角形有什么思路?做高有什么技巧?解斜三角形的条件?方法?学生总结做高的技巧,设未知数的技巧等都很到位。通过不断追问、提问,引导学生将解题技巧、思想方法由隐性的感知变为显性的认识。
学生学习表现积极,学习状况真实有效,学生学习投入度达98%以上。在这节课当中,学生积极配合,主动学习,善于表现,热情高涨,兴趣盎然,说明于老师在平时教学中善于激发学生的数学学习兴趣,注重培养学生的数学学习习惯和学习品质,为学生实现高质量的有效学习奠定了良好的基础,培养了他们自主、合作学习的能力。
以上是教师开发使用课堂观察量表进行观评课的实例,每位教师分别结合学科特点和个体需要、学科组教研需求等方面,选定一个视角进行课堂观察。科学客观地使用观察量表,做好记录。观课结束后,根据量表的数据统计,分别从质和量两个方面进行描述,以往的听评课基本是用定性的方法,我们又融入了定量的分析,让这两种方法有机地结合起来,让观察活动更有说服力。课堂观察便实现了评课不再是评“老师”,而是改进课堂,提升学生的自主学习能力。
