看跌看涨期权平价关系的延伸
前面所讨论的都是欧式期权在没有股利发放情形下的看跌看涨期权平价关系,那么在股票有股利情况下或是在期货期权以及美式期权时,看跌看涨期权平价关系会变成何种情况呢? 以下分成四种情形来讨论。
一、在有股利的情况下,欧式看跌看涨期权平价关系
在有股利的情况下,欧式看跌看涨期权平价关系如公式4-3所示:
C-P=S-D(1+r)-t-K(1+r)-T (4-3)
我们知道股利的发放会降低股价,也就是说股利是股价的减项。因此,在欧式看跌看涨期权平价关系上,只需将公式4-1右边部分的股价减掉股利的折现即可。例如假设在距现在还有t年的时候,发放D元的股利,将D元折现为目前的现值,所以等价公式就变成C-P=S-D(1+r)-t-K(1+r)-T。如果在期权存续期间有发放一次以上的股利,那么同样将所有股利折现到现在,然后由目前股价扣掉此项即可。
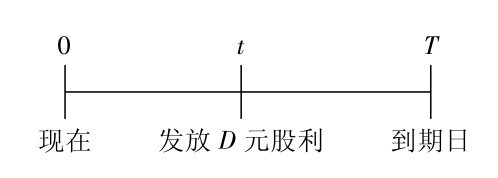
【例题3】 假设鸿海电子公司目前股价为110元,预计半年后要发放4元钱的现金股利,假设期权还有1年到期,执行价格为100元的鸿海欧式看涨期权价值为20元,则条件相同的欧式看跌期权合理价格为多少(假设无风险利率为6%)?
解: 由公式4-3可得:
C-P=S-D(1+r)-t-K(1+r)-T=110-4(1+0.06)-0.5-100(1+0.06)-1=11.77
因为C=20,所以P=20-11.77=8.23。
连续股利下看跌看涨期权平价关系公式
如果不知何时发放股利,但大约知道股利率(dividend yield)为δ,则公式可大致调整为:
C-P=S(1+δ)-T-K(1+r)-T
或连续复利
C-P=Se-δT-Ke-r T。 (4-4)
【例题4】 根据CBOE交易的数据显示,S&P 500指数期权(代号SPX),4月到期, K=1160的看涨期权、看跌期权分别为12.5及8.4; S&P 500指数为1164.2,试验证公式4-4(美国无风险利率及股利率假设为1%,还有15天到期)。
解:已知C=12.5、P=8.4、r=2%、δ=2%、T=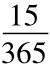
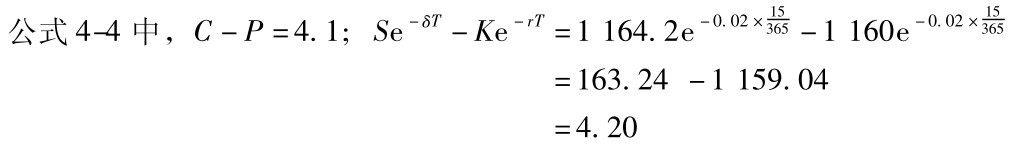
左右两边相差0.1,很接近,所以符合平价理论。
【例题5】 根据我国台湾期货交易所某一天的事务数据,执行价格为8000的台指期权看涨期权及看跌期权分别为125及121、大盘指数7992,请验证看跌看涨期权平价关系。(假设年利率1%,现金股利率2%,距期满日还有20天)
解: C-P=125-121=4
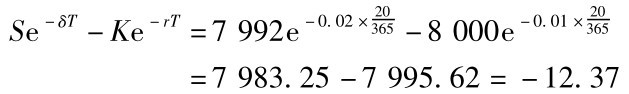
左右两边相差16.37,所以台指期权不符合看跌看涨期权平价关系。[5]
二、在没有股利的情况下,美式的看跌看涨期权平价关系
美式看涨期权会被提前履约的原因,主要是因为股利的发放。因为提前履约,拿到股票才能获得股利(但也损失时间价值),因此在没有股利的情况下,没有理由提前履约而损失时间价值,所以美式看涨期权和欧式看涨期权价格是一样的。但是,看跌期权就不同,美式看跌期权仍可能会有提前履约的情形,尤其在股价很低时,时间价值趋近于0,提前履约比较有利,因为可以提前拿到执行价格K,赚取K的利息。因此,美式看跌期权的价值会大于或等于欧式看跌期权。于是,美式看跌看涨期权平价关系变成一个有上下区间的不等式:
S-K≤Ca-Pa≤S-K(1+r)-T (4-5)
其中,Ca为美式看涨期权,Pa为美式看跌期权。
这个不等式的右边,上限就是公式4-1的看跌看涨期权平价关系的等式右边。但是,下限会比较低,等于S-K。[6]
三、在有股利的情况下,美式看跌看涨期权平价关系
在有股利的情况下,美式看跌看涨期权平价关系如公式4-6所示:
S-D(1+r)-t-K≤Ca-Pa≤S-K(1+r)-T (4-6)
美式期权在有股利发放的情况下,因为股利的发放会降低看涨期权的价值,提高看跌期权的价值,因此看涨期权看跌期权相对价格的下限会再下降,即公式4-5之S-K,下降为公式4-6的S-D(1+r)-t-K。
四、看涨期权看跌期权期货平价理论
根据提到的看跌看涨期权平价关系,知道看涨期权和看跌期权的相对价格,应该等于股价减去目标资产的折现。如多样的资产改为期货即期货期权的看涨期权及看跌期权的价格也有这样的关系,我们称为看涨期权看跌期权期货平价理论(put-call futures parity),以公式表示如下:
CF-PF=(F-K)e-r T (4-7)
其中: CF为期货看涨期权价格,PF为期货看跌期权价格,F为期货价格,K为执行价格。
由公式4-7可以看出,平价时期货看涨期权的价格等于期货看跌期权的价格。
另外,看跌看涨期权平价关系也可写成现货看涨期权看跌期权和期货之间价格的关系:
C-P=(F-K)e-rt (4-8)
其中,C、P分别指现货看涨期权、看跌期权的价格。将公式4-7及4-8结合可得:
C-P=CF-PF (4-9)
即欧式现货看涨期权看跌期权的相对价格等于期货看涨期权看跌期权的相对价格。这很容易懂得,因为欧式现货看涨期权和期货看涨期权的价值是相等的,同理欧式现货看跌期权与期货看跌期权是相等的。
【例题6】 如例题5的资料,假设已知,4月份台指期货的成交价格为8007点,请验证看涨期权看跌期权期货平价理论。
解: 已知C-P=4
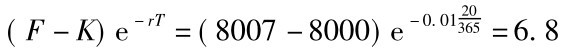
平价理论左右两边差异不大,所以台指期权符合看涨期权看跌期权期货平价理论。
此例说明台指期权和台指期货的关联性比台指现货来得大。这是因为期货商在买卖台指期权时,是利用台指期货来对冲。现货指数因无法交易,所以和台指期权的连动性就比台指期货差。[7]
