多期二项式定价法
上一节讨论的方式是针对股价只上涨或下跌一次的情形,但是只有一期的情形,并不足以反映全貌,因此以下将先介绍两期模型,再进而推导多期模型。
一、两期模型
假设股价在期权到期前有两次上涨或下跌的机会,如图18-2所示。股价在第二期有上涨2次的Suu,上涨一次及下跌一次的Sud及下跌二次的Sdd,其对应的看涨期权价值分别为Cuu、Cud及Cdd。
看涨期权两期模型的公式可以表示如下:
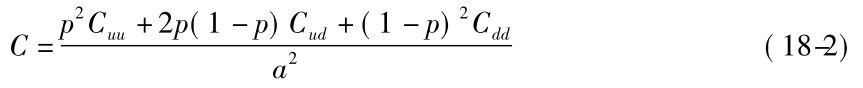
看涨期权两期模型公式18-2 可以由公式18-1 单期推导出来。由于Cu=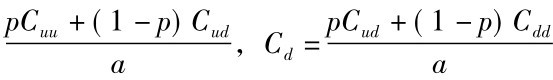 ,将Cu、Cd代入公式18-1,即可得到公式18-2,此部分留于本章习题。另外也可以由Cuu、Cud、Cdd往前推而得到Cu、Cd; 然后由Cu、Cd再推出C。
,将Cu、Cd代入公式18-1,即可得到公式18-2,此部分留于本章习题。另外也可以由Cuu、Cud、Cdd往前推而得到Cu、Cd; 然后由Cu、Cd再推出C。
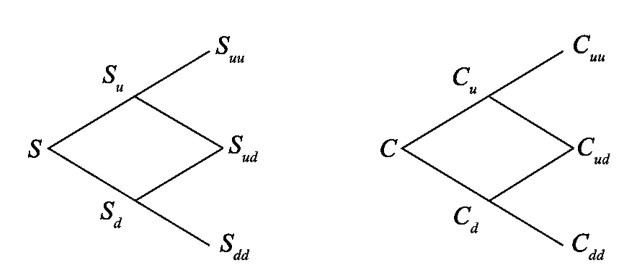
图18-2 两期模型
【例题2】 假设目前股价S=100,看涨期权执行价格K=100,还有1年到期,每半年股价变动一次,另假设u=1.1,d=0.95,年利率为10%,求此欧式看涨期权的价格。
解: 根据上面的说明,有两种计算方法可以得到看涨期权价值:
解法1: 直接利用公式18-2,求出期初看涨期权价格:
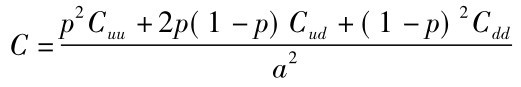
所以
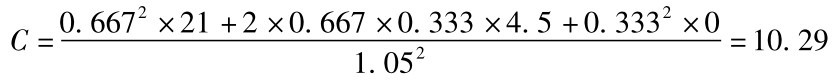
解法2: 由后往前回推的方法: 即为由树形图一步一步反推出期初看涨期权价格。由上述资料可知:
Su=100×1.1=110
Sd=100×0.95=95
Suu=110×1.1=121
Sud=110×0.95=104.5
Sdd=95×0.95=90.25
因此 Cuu=max(0,121-100) =21
Cud=max(0,104.5-100) =45
Cdd=max(0,90.25-100) =0
Δt=0.5,r=10%
又a=erΔt=e10%×0.5=1.05(或a=1+rΔt=1+10%×0.5=1.05)。
另外
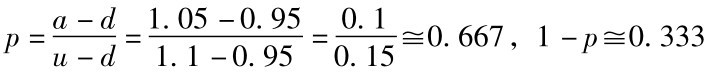
所以先求出:
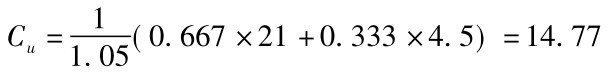
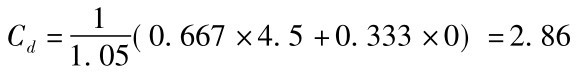
由此可知:
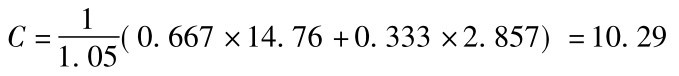
所以,最后求得看涨期权价格为10.29。图18-3为股价展开及期权回推的树形图。
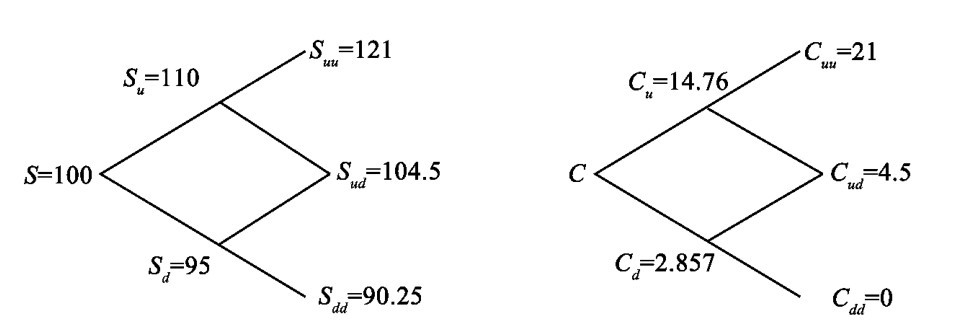
图18-3
二、二项式多期定价公式
当n为多期时,譬如n=10,表示股价在期权到期前有10次上涨或下跌的机会,二项式看涨期权的一般公式为:
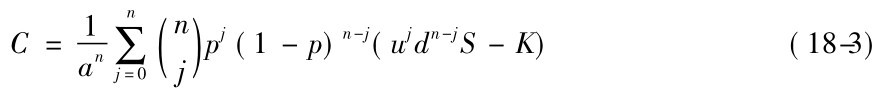
其中,n为分割期数,j为上涨次数,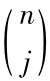 为从n中抽出j的组合次数。
为从n中抽出j的组合次数。
因此,根据公式18-3便可很快由股价求出看涨期权公式,不需要一期一期地折现回来,亦即不需要处理中间的节点。当n愈大,即股价切割愈细时,公式18-3会愈接近理论值,如图18-5所示。[3]
