实质选择权
传统的投资理论中，探讨厂商的投资决策法则，大部分是采用净现值法(net present value，NPV)，或称现金流量折现法(discount cash flow，DCF)。此理论主要是指当厂商的投资计划所获得的预期收益现值大于预期总成本之现值，即投资计划的净现值NPV大于0时，表示该投资计划是可行的; 反之，当净现值小于0时，表示此投资计划不可行。一般净现值的求法可用下列公式表示:
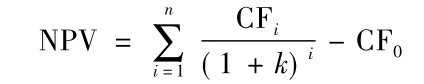
其中，CFi表示第i期的净现金流入，k为要求报酬率，CF0表示期初投入金额。如果NPV＞0，表示该计划值得投资; NPV＜0，表示不值得投资。
然而，以NPV法衡量决策有一些缺点，包括:
传统的NPV法假设投资计划必须维持至计划生命期限(譬如5年)。但实际上，管理者在5年计划执行中的某些时点，可以依当时的市场情况，弹性地中途终止计划，抑或增加或减少生产量或规模大小。此外，传统的NPV法假设计划要马上执行。但实际上，有些计划的执行具有可延迟的弹性，可以等到市场信息较充足时，再决定是否要投入资金执行此计划。另外，要求报酬率k的设定也是令人困扰的。
鉴于传统的NPV的缺失，有些学者尝试由期权的观点，来探讨投资计划中的弹性(如中止、放弃、延迟等的弹性)，而发展出所谓实质选择权分析法(real option approach)。实质选择权分析法便是用来衡量这些投资计划中弹性的价值，而以扩张的NPV(expanded NPV)或称广义的NPV来弥补传统的NPV法(static NPV)的缺失。这些弹性有些是计划本身便具有的，譬如，扩充规模、放弃继续投资等; 或者是由对方所赋予的权利，比方说延迟投资等。以下利用公式来表示实质选择权分析法下的扩张NPV法和传统NPV法的关系:[3]
扩张的NPV=传统的NPV+实质选择权价值 (20-17)
此处扩张的NPV为实质选择权分析法下的NPV，即扩张的NPV等于传统的NPV加上实质选择权的价值(即弹性的价值)。
对此，读者一定会纳闷，为何称此种分析方法为实质选择权分析法呢? 前面介绍过的期权包括股票期权、外汇期权、债券期权，其目标资产均为金融资产，通称为金融期权(financial option)。由于投资计划大多牵涉土地、厂房、矿产等计划，都与不动产(real estate)有关，由于目标资产为不动产等，因此，这些期权就称为实质选择权。以这些实质选择权的概念作为投资决策的出发点，便称为实质选择权分析法。
一般将这种投资决策的弹性，即实质选择权分为改变营运规模期权(option to alter operating scale)、放弃期权(option to abandon)、延迟期权(option to defer)、延续性投资期权(time-to-build option)、转换期权(option to switch)、成长期权(growth option)及多重交互影响期权(multiple interacting option)等，现简单举例介绍。
一、改变营运规模期权
假如厂商在投资计划执行中，当市场情况比原先预期还要好时，厂商可以有弹性地选择扩大(expand)生产规模; 反之，若市场的状况差，厂商可以缩小(contract)原来的生产规模。若厂商因投资所产生的收益不够支付变动成本，则厂商可以选择暂时终止生产，等到市场情况好转，再重新动工，即厂商拥有暂时停工再重新开始的期权(shut down and restart)。
二、放弃期权
假若市场情况不如预期，则厂商可选择永久放弃此投资计划，并将已投资的机器设备以残余价值卖出。因此，投资计划具有放弃期权(option to abandon)的效果。
三、延迟期权
假设厂商拥有一个可以延迟1年投资的租约或是权利，则投资者可以等1年后，从市场获得更多、更新的信息后，再决定是否要投资此计划，故又称为等待期权。延迟期权(option to defer)可有效降低投资环境的不确定风险，以免成本一投入，变成沉没成本而无法收回。
四、延续性投资期权
假设投资计划是由一系列的投资支出所组合的阶段性投资项目，每个阶段有其必要的投资支出。若市场新信息显示未来的市场不乐观，投资厂商可以选择中途退出此一投资计划，以免蒙受更大损失，因此，延续性投资期权(time-to-build option)又可称为违约期权(default option)。每一投资阶段皆可视为一期权，其目标物为后续阶段投资所产生的价值，此类期权就是第十七章提过的复合期权(compound option)。这种期权如同以前我们提过的购买预售屋时分期支付房屋价款，如果发现房价大幅下跌，可以选择放弃继续支付屋款的例子。此种违约期权常见于制药、高科技等行业的研究开发计划。
五、转换期权
当厂商面临市场需求改变，或原料、产出的价格变动时，厂商可选择改变其生产投入组合或产出组合，以获取最高利润。例如，当市场原料价格上涨，投资者可选择将原来的生产原料改为比较便宜的原料，以降低成本。或者当产品的价格下跌时，生产者可以将设备转换，改为生产价格较高的他种产品。其中，转换期权(option to switch)是投资者拥有转换的权利，因此具有价值。
六、成长期权
成长期权(growth option)可显现出公司策略运用的重要性。例如许多研究发展(R＆D)计划在现阶段可能无法显现其效益，但若未来发展成功，将会带来可观的收益。此类项目使公司未来的成长机会大增，因此，对公司而言是一成长期权。
七、多重交互影响期权
若投资计划包含多个不同实质选择权，譬如，扩充、放弃、延迟等期权，就是多重交互影响期权(multiple interacting option)。此时，各个期权可能会交互影响彼此的价值，其计算因而比较复杂。
八、加入实质选择权的NPV
在此举一个例子说明如何用二项式模型来求改变营运规模期权的价值。
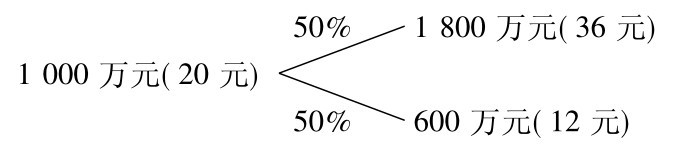
【例题3】 假设有一投资计划，未来有50%的机会有1800万元的收入(当油价每桶上涨到36元)，有50%的机会有600万元的收入(当油价每桶下跌到12元)，如下图。若以必要报酬率20%来折现，则此投资机会的现金流入现值为=1000万元。假设此计划的原始投入成本为1040万元，依照传统净现值法估计，此计划传统的NPV=40万元，则此投资计划不会被执行。但是，假若此时允许此投资计划有一投资弹性，即可以在市场情况好的时候扩充50%的产能，而所增加的支出为400万元，此时的NPV将变为多少呢? 此扩充期权的价值又是多少呢(假设已知目前油价每桶20元)?
解: 我们利用第十八章提过的二项式定价法在风险中性下的模型，求出转换后的概率P。因为风险中性转换的观念可以帮助我们了解实质选择权在投资决策弹性中的定价。
利用风险中性的方法计算目前油价为20元，未来油价为36元与12元的概率为P与1－P。由于d=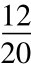
=0.6，u=
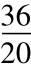=1.8，假设无风险利率为8%，所以P=
=
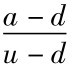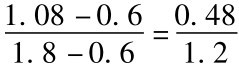=0.4，则1－P=0.6，即收入为1800万元的虚拟概率为0.4，收入为600万元的虚拟概率为0.6，如下图所示。
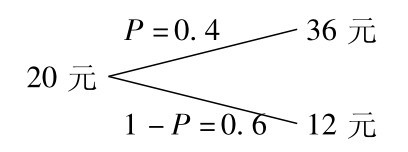
此扩充期权(option to expand，OTE)的价值为max(0.5V－40，0)，以V+表示收入为1800万元，V－表示收入为600万元的情况。以OTE+表示收入为V+时OTE的价值，以OTE－表示收入为V－时OTE的价值，则:
OTE+=max(0.5V+－400，0) =max(0.5×1800－400，0)=max(500，0) =500
OTE－=max(0.5V－－400，0) =max(0.5×600－400，0)=max( －100，0) =0
根据二项式的看涨期权公式18-1，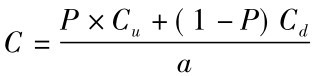
，所以，扩充期权的现值为:
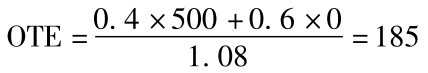
由公式20-17得知，扩张的NPV=传统的NPV+扩充期权=－40+185=145。此时的NPV大于0，其实是一个可以投资的计划。此扩充的弹性价值为185万元，是一项不可忽略的价值。
风险中性假设告诉我们，任何证券的现值为未来期望值以无风险利率的折现，因此，不需要以主观的必要报酬率20%来折现。此外，风险中性假设也不需要事先假定收入为1800万元及600万元的概率(如例题1为50%)，而是由给定的条件推算风险中性下的概率。
本节只是简单介绍实质选择权运用到投资决策分析的简单概念及定价。至于如何正确评估这些实质选择权的价值，或是在多期的情形下如何定价，或是多重交互影响期权如何定价，则属于另外一个较深入的主题，本书不拟在此讨论。由于实质选择权的评估方法比较合乎现实的投资决策弹性，因此，已经有学者尝试以实质选择权的方法，来评估许多各式各样的投资计划，如银行的合并案，有兴趣的读者可以参阅相关文献。