二项式美式期权定价法
由于美式期权具有提前履约的特性，因此，如果提前履约有利，则提前履约所得到的内在价值将会高于原来持续持有欧式期权的价值。所以，第二节欧式期权的运算公式18-3便不能使用，而需要每一期都去比较内在价值和期权继续持有价值，取其较大者。本节除了讨论二项式美式期权定价法外，另外亦讨论u、d的选取，以下举例说明二项式对美式期权的处理。
【例题3】 假设S=100，u=1.1，d=0.95，a=1.05，n=2，求执行价格为100元的欧式看跌期权及美式看跌期权的价格。
解: 分别计算如下:
(1)欧式看跌期权
根据所给资料，上涨概率p=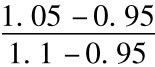
≅0.667，1－p=0.333。将股价及看跌期权展开如下图:
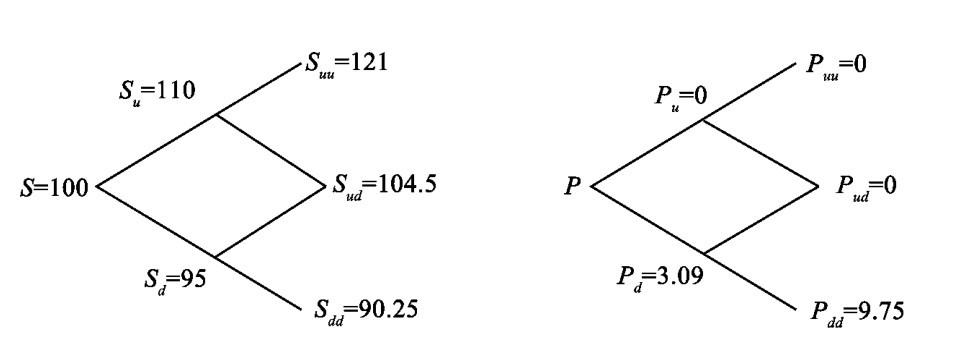
Puu=pud=0，所以Pu=0; Pdd=100－90.25=9.75，所以Pd=(0.667×0+0.333× 9.75)/1.05=3.09，因此: 欧式看跌期权=(0.667×0+0.333×3.09)/1.05=0.98
(2)美式看跌期权
美式看跌期权需考虑提前履约的问题，即比较内在价值与反推出来的看跌期权价值，取其较大者。因为在节点Sd的股价为95元，所以看跌期权内在价值K－S=100－95=5。因为内在价值大于第一期看跌期权求出的价格Pd=3.09元，所以会提前执行，所以取Pd=max(5，3.09) =5元，因此美式看跌期权=(0.667×0+0.333×5)/1.05=1.59，比欧式的0.98大。所以在求美式期权时，需要在每一个节点比较内在价值与二项式反推回来的价值，而取其较大者。[4]
u、d、p的选取
上两节提到假设股价上涨到Su，下跌到Sd的情形。但是并没有讨论到u、d应如何选取才合适。如果u、d、p的设定满足对数正态分布假设，即满足股价报酬分配的平均值及变异数大小的假设，则二项式求得的解会很快收敛到理论值。
一般我们假设:
亦即u=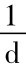
;其中σ为股价报酬波动率，Δt为分割期间，如果1年分为两期，则Δt=
。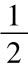