隐含波动率的估计
一、隐含波动率的估计: 二分法及牛顿拉弗森法
隐含波动率在第五章已提过，是将期权的市场价格代入B-S评价公式中，求出市场期权价格内所包含未来股价的波动率。在求算隐含波动率时，我们可以用试错(try and error)的方法，将不同的波动率带入B-S公式中，看哪一个波动率得出来B-S的值和期权的市价之差可以低到±0.1或甚至±0.01，此时的波动率就是隐含波动率。但是，这种方法比较浪费时间，也没有效率。有一种简单的估计方法比较有规则，就是二分法(bisection method)。
(一)二分法
二分法的基本概念是，先猜一个低的波动率(σL)以及一个高的波动率(σH)，将σL、σH代入B-S公式分别算出2个BS值，分别为BSL、BSH，并使市价介于这两者之间。接着再采取σL、σH两个的中间值(σM)，再带入B-S公式求出BSM。如果市价介于BSL和BSM之间，则下一个σ取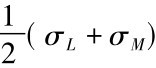
;如果市价介于BSM及BSH之间，则下一个σ取
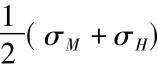。如此重复上述步骤，一直缩小所猜σ的上下范围，直到所猜的BS值与市价的误差小于0.01为止，此时的σ就是所要求的隐含波动率。
另外一种改良的二分法，可以更快找到隐含波动率。其概念是等比例的想法。亦即假设价格差异的比例等于波动率差异的比例，而不是只猜中间的σ。譬如，期权市价和上界值BSH之差为a，市价和下界值BSL之差为b，那么所要猜的下一个σM须满足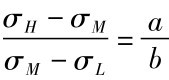
。解等式，则得到:
而前面提到的所求的σM是取中间值，则是假设σH－σM=σM－σL。
(二)牛顿拉弗森法
另一种求隐含波动率的方法称为牛顿拉弗森法(Newton-Raphson method)。它的概念是利用微积分切线斜率来逼近期权市价。譬如先猜一个σ1，则下一个要猜的σ2为:
其中Cm为市价，C(σ1)为代入σ1的BS值，C'(σ1)为C对σ1的一阶导数，即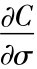
，等于vega。如此一直猜σ3，σ4，…，直到Cm－C(σi)之差小于0.01，此时的σ即隐含波动率。这个方法比二分法还要快。
二、采用何种隐含波动率为代表
我们曾经提到，不同的执行价格有不同的隐含波幅，即所谓的笑状隐含波幅。那么应该采用何种契约的隐含波幅，作为目标指数波动率的代表呢? 有一些学者做了以下不同的建议:
1．Latane and Rendleman(1976)以每一契约价格对波动率的一阶偏导数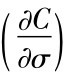
，来作为各隐含波幅的权数，而后加总成为单一的隐含波幅，作为预期波动率的测度。
2．Beckers(1981)认为，平价的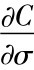
一般最大，他建议采用平价的隐含波幅作为代表及对未来波动率的预测。
3．Chiras and Manaster(1981)以每一期权契约价格对波动率的弹性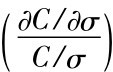
，即相对变动率作为权数来加总隐含波幅。
4． Whaley(1981)利用回归的方法，求出可使总误差平方最小的隐含波幅作为代表的预期波幅，即:
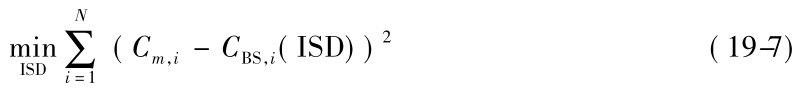
其中，Cm，i和CBS，i(ISD)分别为第i个看涨期权市价及某个ISD下B-S理论价格。
5． Day and Lewis(1988)建议采用各期权合约的交易量作为权数来加权。他们认为交易量越大，越可以降低异步交易(nonsynchronous trading)的情形，同时减少买卖价差(bid-ask spread)。
6． 芝加哥期权交易所在1993及2003年分别编制了两种波动率指数VIX来代表整个指数的波动率。前者采用8个平价附近的看涨期权、看跌期权的隐含波动率加权就是采用平价的隐含波动率; 后者采用所有价外的看涨期权、看跌期权市值，不用期权评估公式，而是直接利用转换公式加总而得。中国台湾期货交易所也在2006年引进VIX可以作为未来现货指数波动率的预期值。