4.3.2  一元线性回归分析

回归分析按照涉及的自变量的多少，可分为一元回归分析和多元回归分析。按照自变量和因变量之间的关系类型，则可分为线性回归和非线性回归。如果在回归分析中，只包括一个自变量和一个因变量，且两者的关系可用一条直线近似表示，则此种回归分析称为一元线性回归分析。对于独立试验得到的n对观测结果：（x₁，y₁），（x₂，y₂），…，（x_n，y_n），一元线性回归的回归模型可表示为

y=a+bx （4-30）

式中 y——因变量；

x——自变量；

a、b——回归系数，其计算式分别见式（4-32）和式（4-31）。

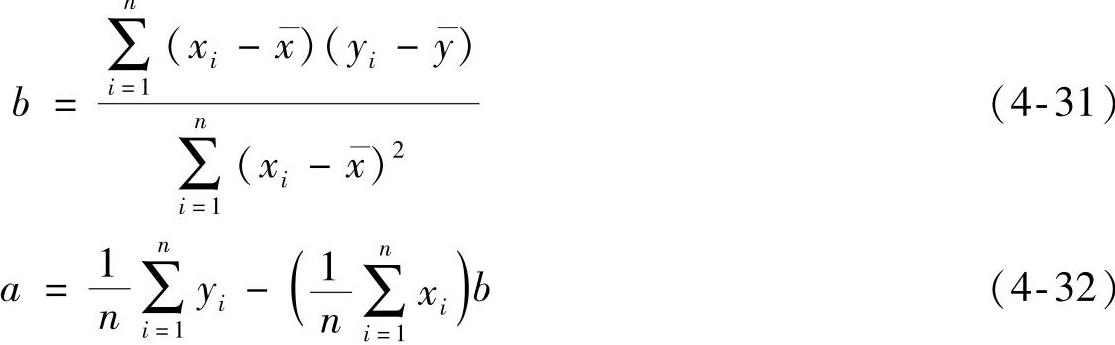
将a、b代入回归模型式（4-30）中，即可得到y的估计量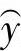为

为了判定回归分析是否对观测数据进行了完好地描述，一般用回归判定系数r²来进行判定，其定义为

|r|越接近于1，就表明建立的回归方程越接近于实际观测数据。|r|=1，x与y是完全确定的线性相关关系；|r|＞0.7，x与y为高度线性相关；0.3＜|r|≤0.7，x与y为中度线性相关；|r|≤0.3，x与y为低度线性相关；|r|=0，x与y无线性相关关系。本书附录I给出了相关系数检验表，表中的数值叫作相关系数的起码值。