8.2.2  弯曲试验原理

8.2.2 弯曲试验原理

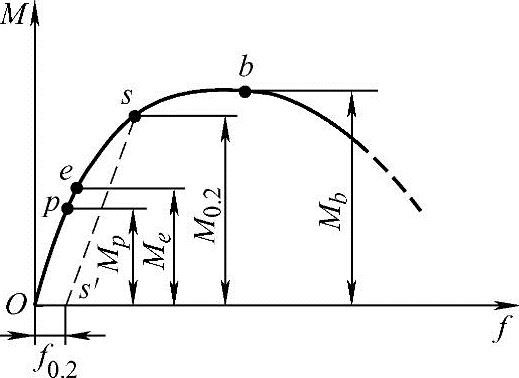
图8-12 弯矩-挠度曲线

做弯曲试验时，将圆形或矩形横截面试样放置在一定跨距L_S的支座上，进行三点弯曲或四点弯曲加载，通过记录弯矩-挠度（M-f）或弯曲力-挠度（F-f）关系曲线，确定金属在弯曲力作用下的力学性能。试样上的外力垂直于试样的轴线，并作用在纵向对称面内，试样的轴线在纵向对称面内弯曲成一条平面曲线的弯曲变形称为平面弯曲。典型的试样中点处的弯矩-挠度曲线如图8-12所示。

从图8-12中可以看出，当试验进行到p点时，弯矩M与挠度f仍保持正比关系；进行到e点时，挠度仍为弹性变形，超过e点，则将产生一定的塑性变形；达到b点时，弯矩为最大值。超过此点，弯矩将逐渐下降，直至试样断裂。

弯曲试验常用两种加载方法：在支座中点集中加载的方法，称为三点弯曲，如图8-13a所示；通过四点弯曲加载装置的两个加载辊将载荷施加在试样上，称为四点弯曲，如图8-14a所示。

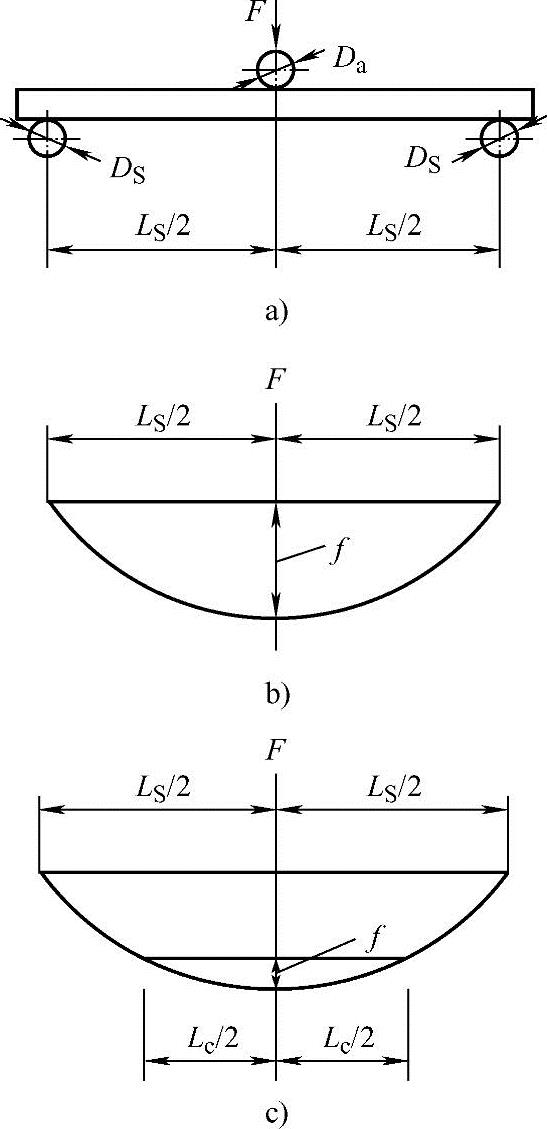
图8-13 三点弯曲试验示意图

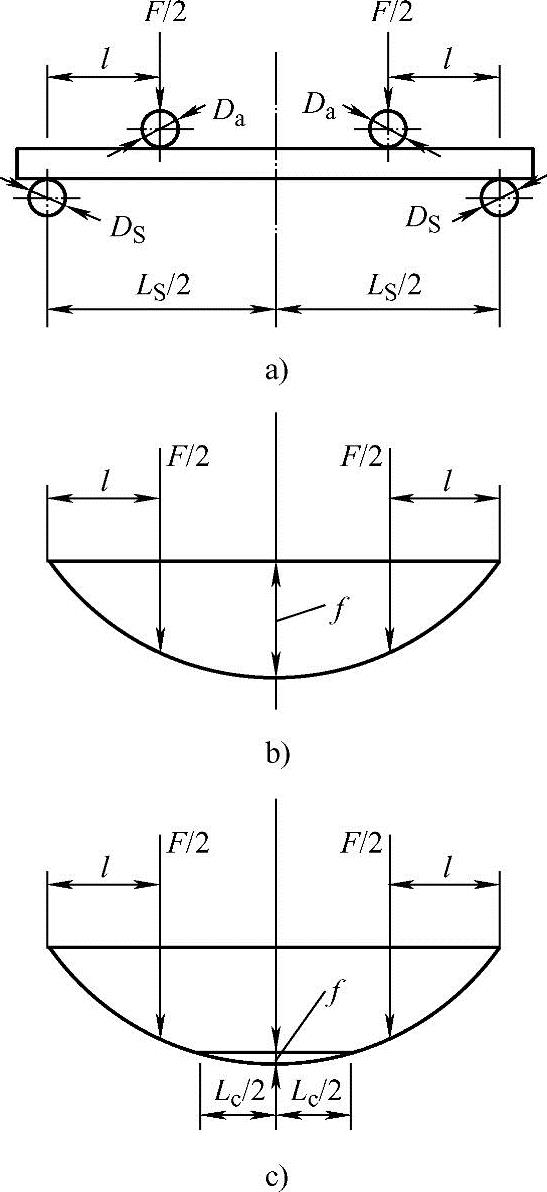
图8-14 四点弯曲试验示意图

试样弯曲时，一般承受弯矩和剪力。在试样的横截面上一般有弯矩产生的正应力和剪力产生的切应力。

1.弯曲试样上承受的弯矩和剪力

（1）三点弯曲试样 三点弯曲试样上的弯矩和剪力如图8-15所示。

在试样的左半段：

弯矩M₁=FX/2 （0≤X≤L_S/2）

式中 X——三点弯曲试样上的考察点到左支座的距离（mm）。

剪力Q₁=F/2 （0＜X＜L_S/2）

在试样的右半段：

弯矩M₂=F（L_S-X）/2 （L_S/2≤X≤L_S）

剪力Q₂=-F/2 （L_S/2＜X＜L_S）

在试样的中点弯矩最大，可按式（8-8）计算。即

M_max=FL_S/4 （8-8）

（2）四点弯曲试样 四点弯曲试样上的弯矩和剪力如图8-16所示。四点弯曲试验中，两弯曲力均为F/2，两力臂均为l，两力臂之间弯矩最大，可按式（8-9）计算。即

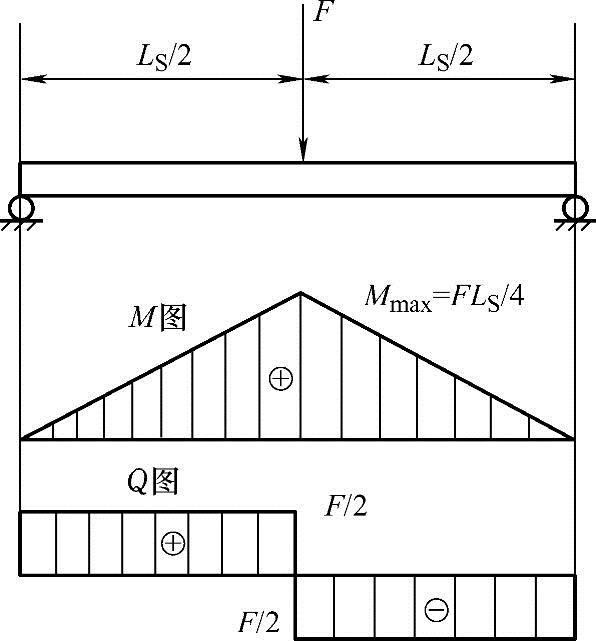
图8-15 三点弯曲试样的弯矩图和剪力图

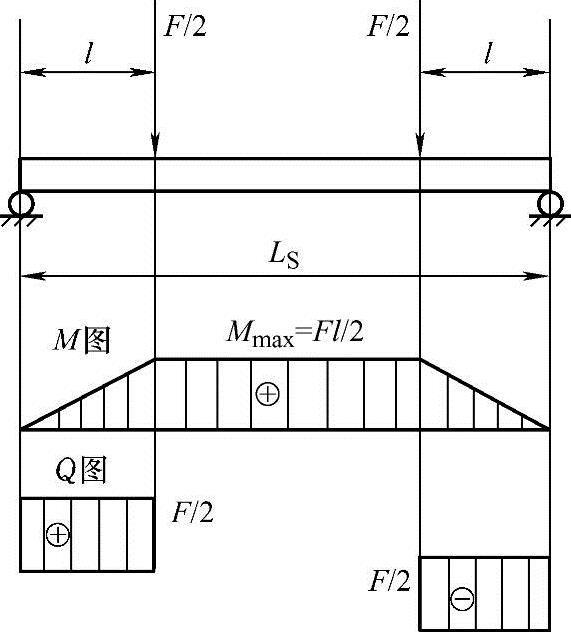
图8-16 四点弯曲试样的弯矩图和剪力图

M_max=Fl/2 （8-9）

四点弯曲试样的施力点与支座之间的剪力Q按式（8-10）计算。即

Q=F/2 （8-10）

在四点弯曲试验的两弯曲力之间的各横截面上只有均匀分布的弯矩M，而无剪力Q，称为纯弯曲。试样通常会在该长度上的任何薄弱处破坏。而三点弯曲试验总是在试样中点处及其附近破坏。

在四点弯曲试验和三点弯曲试验的弯曲力与支点之间的各横截面上同时有弯矩M和剪力Q，称为剪切弯曲。

2.弯曲试样横截面上的应力与分布

（1）弯曲试验时的正应力 材料力学假设：试验材料是均匀、各向同性的，变形是弹性的；变形前后试样的各横截面都是平面，且与试样轴线垂直。通过对图8-17所示弯曲试样的正应力与弯矩的关系进行变形分析，可以得出弯曲试样在弹性变形范围内，横截面上任一点正应力σ按式（8-11）计算。即

σ=MY/I （8-11）

式中 M——弯矩（N·mm）；

Y——横截面上任一点到中性轴的距离（mm）；

I——试样横截面对中性轴的轴惯性矩（mm⁴），是仅与横截面的形状和尺寸有关的几何量。

式（8-11）表明，弯曲试样横截面上的正应力σ与弯矩M、到中性轴的距离Y成正比，与轴惯性矩I成反比；Y为正值时试样受拉，Y为负值时试样受压，试样的最外层正应力最大。试样的正应力分布如图8-18所示。

试样的最外层正应力最大。即

σ_max=M_maxY_max/I=M_max/W （8-12）

式中 W——弯曲试样截面系数（mm³），仅与横截面的形状和尺寸有关的几何量，W=I/Y_max。

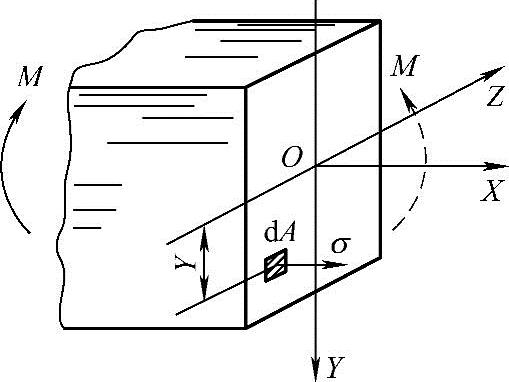
图8-17 弯曲试样的正应力与弯矩的关系

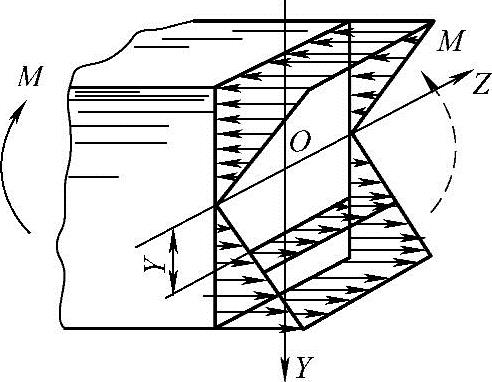
图8-18 试样的正应力分布

对于宽度为b、高度为h的矩形截面试样，有I=bh³/12；W=bh²/6。

对于直径为d的圆形截面试样，有I=πd⁴/64；W=πd³/32。

（2）弯曲试验时的切应力 试样剪切弯曲时，横截面上不仅有正应力σ，还有切应力τ。材料力学假设：横截面上全部切应力的方向都平行于被它们所平衡的剪力Q；距中性轴等距离处的切应力相等。通过对图8-19所示弯曲试样横截面上Q及τ的分布的关系进行变形分析，可以得到：

矩形弯曲试样（宽度为b，高度为h）的横截面上任一点的切应力，有：τ=3F（1-4Y²/h²）/（4bh）；在中性面处（Y=0），切应力最大，τ=τ_max=3F/（4bh）；在上下表面处（Y=±h/2），τ=τ_max=0。

圆形弯曲试样（直径为d）的横截面上任一点的切应力，有：τ=8F（1-4Y²/h²）/（3πd²）；在中性面处（Y=0），切应力最大，τ=τ_max=8F/（3πd²）；在上下表面处（Y=±d/2），τ=τ_max=0。

试样的切应力分布如图8-20所示。

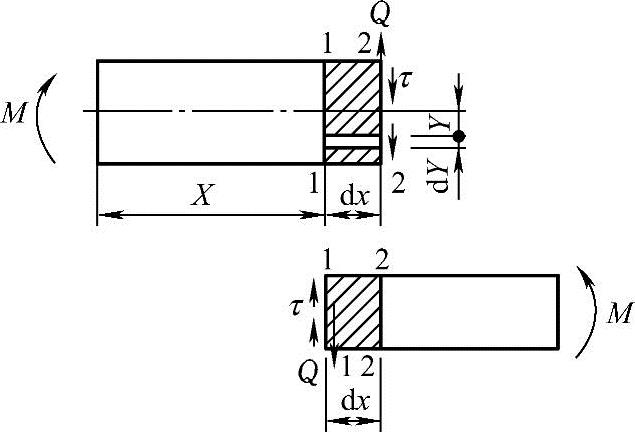
图8-19 试样横截面上Q和τ的分布

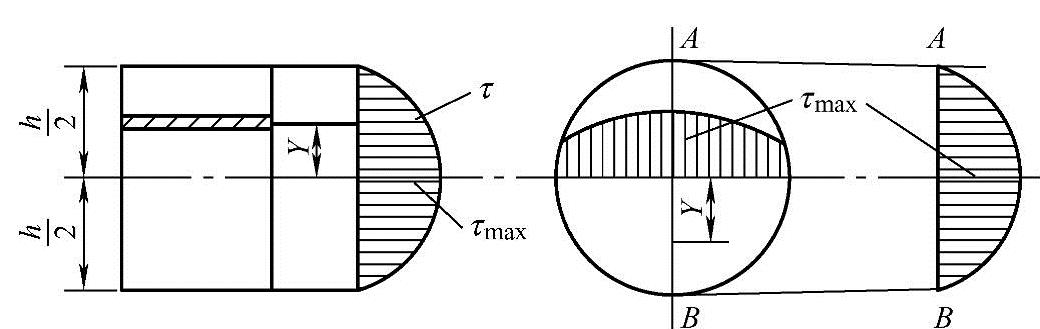
图8-20 试样的切应力分布

（3）三点弯曲试验时试样横截面上的最大正应力和最大切应力的关系

1）矩形截面试样

σ_max/τ_max=2Ls/h （8-13）

2）圆形截面试样

σ_max/τ_max=3Ls/d （8-14）

弯曲试验测定正应力σ时，要尽量减小切应力τ的影响。通常会保证试样有一定长度，如取L_S=10d（或L_S=16h），则三点弯曲时，切应力的影响小于5%。

（4）弯曲试样的挠度 由材料力学可知，梁的弯曲在弹性范围内，忽略剪力的影响时，挠度f与转角θ、弯矩M之间的关系为：挠度f的一次积分等于转角θ，挠度f的二次积分等于弯矩M除以EI。

通过积分可以得到：三点弯曲时，试样左半段挠度有：f₁=-FX（3L²_S-4X²）/（48EI）；试样中点处挠度最大，即

f_max=FL³_S/（48EI） （8-15）