11.7.2P-S-N曲线的绘制
研究表明,最适宜表达对数疲劳寿命x分布规律的曲线是“正态分布概率密度曲线”,也叫作“高斯曲线”。

式中 e——自然对数的底,e=2.718;
μ——母体平均值;
σ——母体标准差。
当μ和σ已知时,函数f(x)也就确定了。按照这个函数绘制出的正态分布概率密度曲线如图11-20所示。
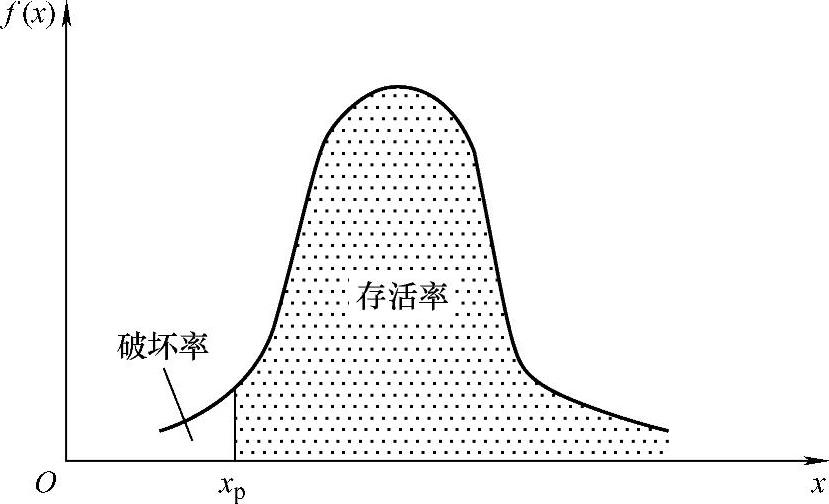
图11-20 正态分布概率密度曲线
当已知对数疲劳寿命x=lgN的正态分布概率密度曲线时,给定任意一个xp值,即可知道xp以右曲线与横坐标轴所包围的面积,如图11-20所示。
如以ξ表示作为随机变量的对数疲劳寿命,则该部分面积为随机变量ξ大于xp的概率P(ξ>xp)。反之,当指定某一概率,也可确定出对应的xp值。如指定这个概率为90%,即随机变量ξ大于xp的概率P(ξ>xp)为90%,则意味着:100个试件中,有90个试件的对数疲劳寿命高于xp,因此这个指定的概率90%,称为“存活率”。由于概率密度曲线与横坐标轴之间所包围的面积为1,图11-20中xp左边的空白面积为10%,它表示随机变量ξ小于xp的概率P(ξ<xp),因此10%相当于“破坏率”。存活率P(ξ>xp)和破坏率P(ξ<xp)之间存在着以下关系
P(ξ>xp)+P(ξ<xp)=100% (11-23)
由图11-20可见,存活率取得越高,xp值就越小。在航空产品设计中,存活率一般都取得很高。对应于这种高存活率的对数疲劳寿命叫作对数安全寿命。譬如,存活率常常取99.9%,此时x99.9就叫具有99.9%存活率的对数安全寿命。而“安全寿命”N99.9就是x99.9的反对数。即
N99.9=lg-1x99.9 (11-24)(https://www.daowen.com)
具有99.9%存活率的安全寿命N99.9的含义是:在1000个产品当中,有999个的寿命都高于安全寿命N99.9,只有一个未达到安全寿命N99.9而提前发生破坏。更确切地说,母体中有99.9%的个体寿命高于N99.9,有0.1%的个体寿命低于N99.9。存活率为P的对数安全寿命xp计算公式为
xp=μ+upσ (11-25)
式中,up可通过查表11-4获得。
表11-4 标准正态偏量数据

威布尔分布概率密度函数的优点在于存在最小安全寿命,即100%可靠度的安全寿命。按照正态分布理论,只有当对数安全寿命xp=lgNp趋于-∞时,即Np=0时,可靠度才等于100%。显然,这是不符合实际情况的,这也是正态分布理论的不足之处。
采用威布尔分布理论,在极高可靠度范围(99.99%~100%)内所给出的安全寿命或最小安全寿命仍然比较符合实际情况。但由于威布尔分布概率密度函数的数学形式较繁,使得它在一些统计推断方面受到限制。
在同一循环载荷作用下,各试件疲劳寿命N的分布规律,可以由以下威布尔分布概率密度函数表示。即
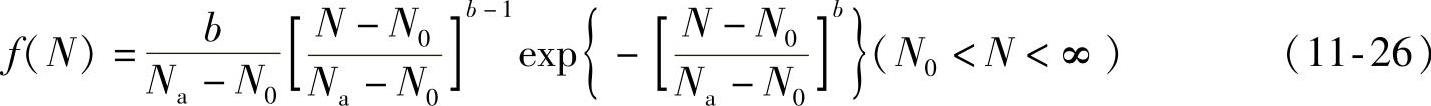
式中 N0——最小寿命参数;
Na——特征寿命参数;
b——威布尔形状参数(斜率参数)。
由于威布尔分布概率密度函数中包含三个待定参数,因此它能更完善地拟合试验数据点。
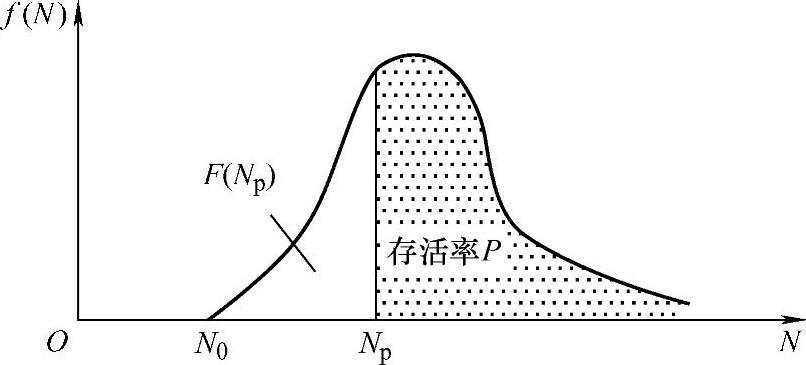
图11-21 威布尔分布概率密度曲线
当b=1时,f(N)为一简单的指数分布概率密度函数。当b=2时,f(N)为一瑞利分布概率密度函数。当b=3~4时,f(N)接近正态分布概率密度函数。曲线高峰通常偏斜向左,偏斜程度随b而变化。对于b>1的情况,当N=N0时曲线与横坐标轴相交,由图11-21可以看到,存在有大于零的最小寿命值N0。差值(Na-N0)越大,曲线外形越扁平,分散性越大。曲线右端延伸至无限远处,以横坐标轴为渐近线。
根据威布尔分布概率密度函数,求出威布尔变量的分布函数F(Np),即Nξ小于某一数值Np的概率P(Nξ<Np)。
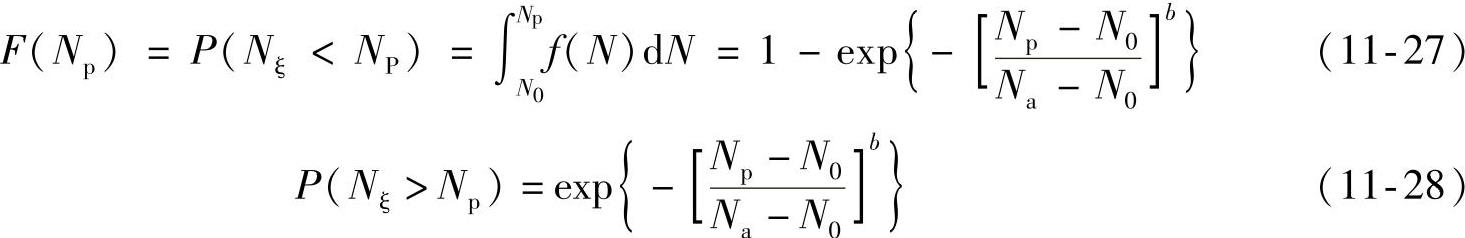
P(ξ>xp)+P(ξ<xp)=100% (11-29)
由图11-20可见,N0是对应存活率100%的疲劳寿命。按威布尔函数分布计算不同存活率的疲劳寿命,显然要比对数正态分布函数复杂得多。
