13.1.3 线弹性断裂力学的几个基本概念
1.裂纹尖端的应力场及应力强度因子K
对裂纹的研究表明：构件在发生脆性断裂的瞬间，裂纹尖端附近的绝大部分都处于线弹性变形状态。应用线弹性断裂力学理论，研究带裂纹体的应力-应变关系。对于Ⅰ型裂纹，裂纹尖端的应力分量如图13-3所示。
线弹性断裂力学的理论分析已经证明，对于上述三类裂纹问题，在裂纹尖端区域（r→0）的应力应变场呈现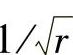
阶的奇异性。用KⅠ、KⅡ、KⅢ分别代表每种裂纹类型的应力场奇异性强度因子，简称应力强度因子，定义为
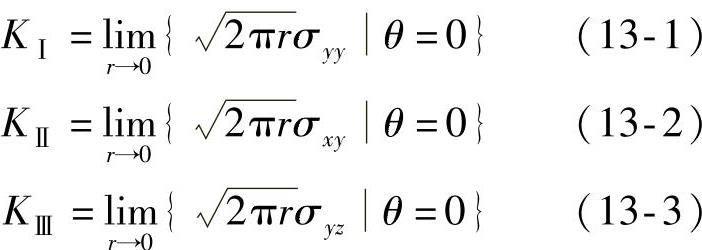
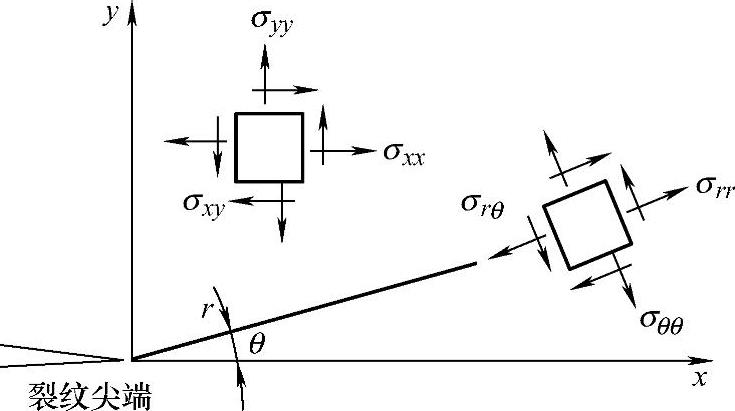
图13-3 裂纹尖端的应力分量
对于主要讨论的Ⅰ型裂纹，裂纹尖端的应力分量为
位移分量为
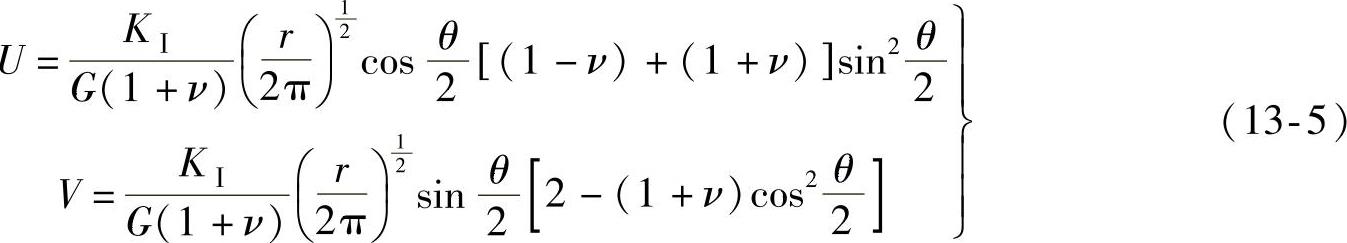
式中 G——材料的剪切模量；
ν——材料的泊松比；
r、θ——图13-3所示的极坐标参量。
由式（13-4）、式（13-5）可以看出：裂纹前缘的应力、应变场完全由应力强度因子K所决定，而K的一般表达式为
式中 a——裂纹长度；
f——无量纲的应力强度因子（或边界修正系数）。
应力强度因子K主要与下列因素相关：
1）试样所受的载荷状况。
2）裂纹长度。
3）试样和裂纹的几何形状。
外加载荷、裂纹长度以及试样的几何形状与尺寸，都只通过应力强度因子K来影响裂尖奇异场的程度，K是表征线弹性裂纹体裂纹尖端奇异性强度的参量。应力强度因子的这一特点使它成为裂纹扩展力的度量和裂纹失稳扩展的准则，在断裂力学和损伤容限设计中起着关键的作用。
2.小范围屈服与K主导
如图13-4所示，若根据线弹性断裂力学理论解，裂纹尖端的应力将趋近于无穷。而实际上这是不可能发生的，在裂纹尖端附近的微小区域内，材料必然进入屈服状态，从而影响周围弹性应力场的分布。
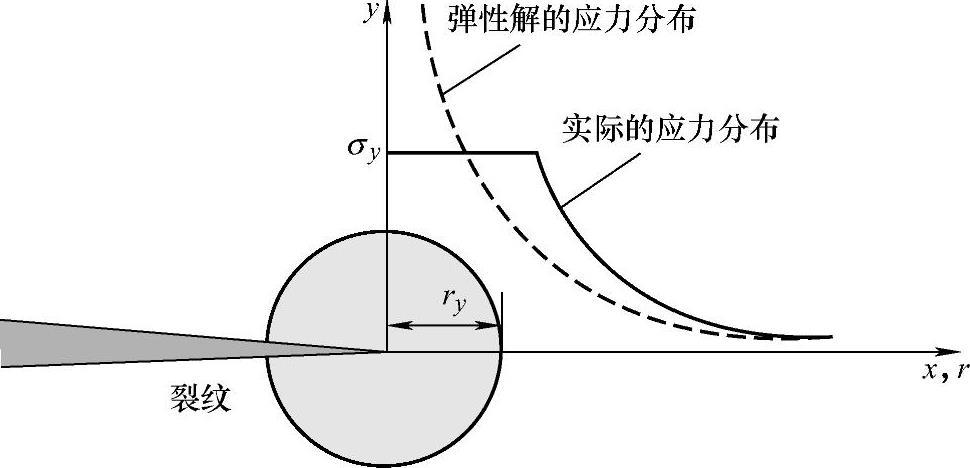
图13-4 裂纹尖端的应力分布
线弹性断裂力学是建立在小范围屈服的基础上的，所谓小范围屈服是指裂纹尖端的塑性区尺寸比裂纹长度或其他特征几何尺寸小得多的情况。一般认为，当裂纹尖端塑性区尺寸ry与裂纹体的最小特征尺寸相比小约1/25时，小范围屈服条件就可得到满足。
如图13-5所示，在裂纹尖端的非弹性区范围内，线弹性解将失去其有效性。但是，只要这个非弹性区比起裂纹体的最小特征尺寸要小得多（即满足小范围屈服条件），则基于线弹性分析得出的裂纹尖端奇异场仍能作为围绕裂纹尖端附近的环形区域的实际场的良好近似。因此，在小范围屈服条件下（ry＜RK），应力强度因子K成为描述裂纹尖端应力应变场的唯一度量，此即所谓的“单参量表征”，即裂纹尖端的力学环境由K唯一决定。
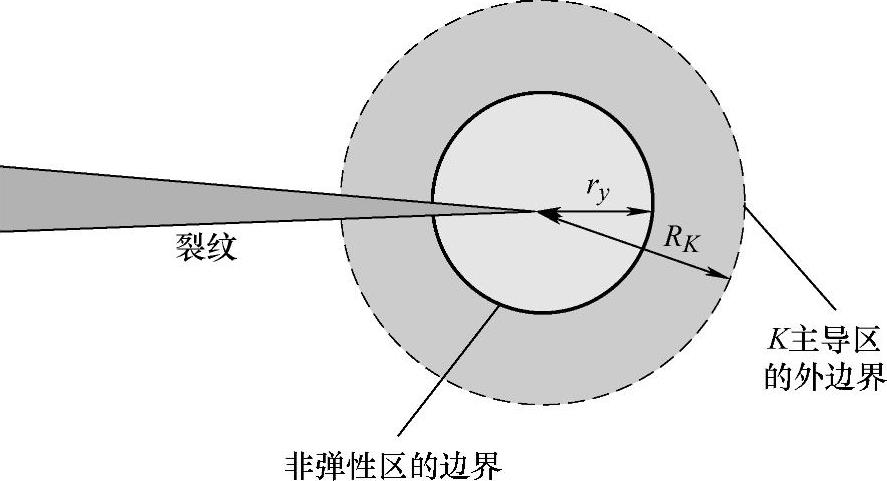
图13-5 裂纹尖端的K主导区
3.平面应变与平面应力
断裂力学所考虑的平面应力或平面应变是指裂纹尖端塑性区内的应力状态。不同厚度的Ⅰ型裂纹，其塑性区尺寸和应力状态是完全不同的。
平面应变状态：当裂纹足够厚时，裂纹尖端沿厚度方向的变形会受到限制，应变主要发生在另两个方向组成的平面内，这就形成了线弹性断裂力学中的平面应变状态。
平面应力状态：当裂纹较薄时，则可能会出现另一种情况，如侧面受载的薄板，垂直于板面方向的应力全为零，应力只存在于板面内，这就是线弹性断裂力学中的平面应力状态。
而介于平面应变和平面应力之间的状态为过渡状态。
工程上通常根据裂纹厚度B来定量区分平面应变、平面应力及过渡状态。
（1）平面应力状态（薄）
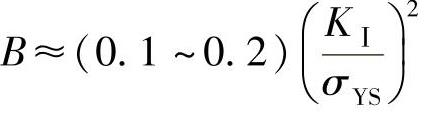
（2）平面应变状态（厚）
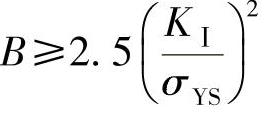
（3）过渡状态
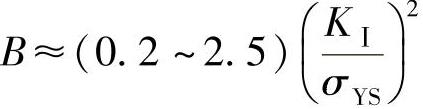
平面应力和平面应变常常可以从断口形貌上得到判别。一般来说，平面应变所对应的裂纹前缘比较平直，断口本身以平断为主，只是接近表面层有很小的斜断口。相反，平面应力所对应的裂纹前缘常呈向前突出的指甲状，斜断口所占比例较大。
4.裂纹尖端的塑性区尺寸及修正
对于平面应力和平面应变状态，其塑性屈服区的形状是不同的，如图13-6所示，其尺寸ry可以按式（13-7）和式（13-8）进行估计。即
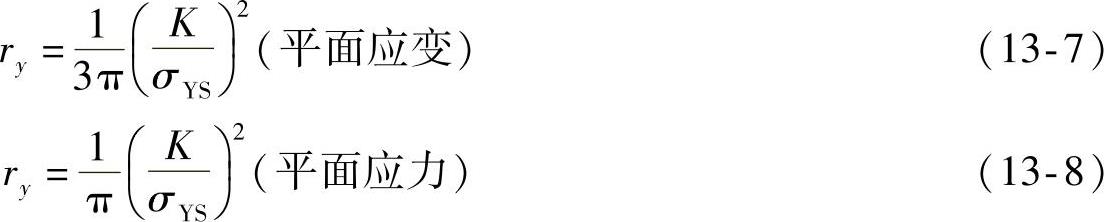
式中 σYS——条件屈服强度。
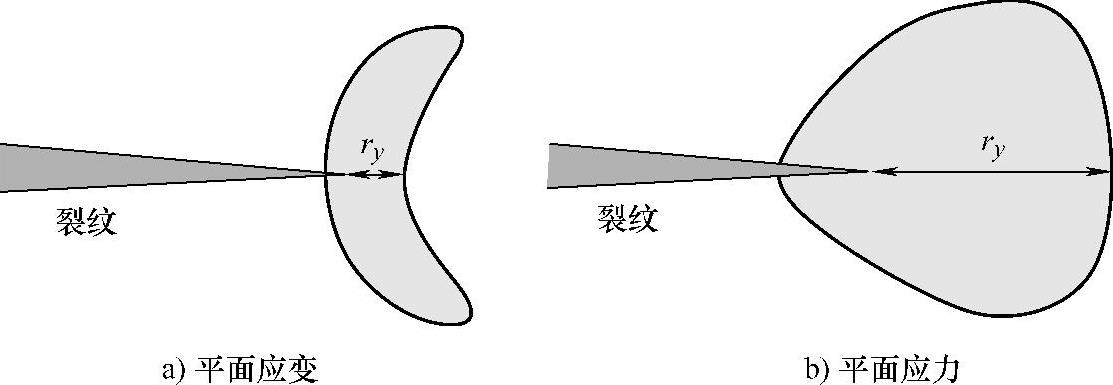
图13-6 裂纹尖端的塑性区
对于平面应变状态而言，若要小范围屈服条件得到满足，则要求
为了避免带裂纹体的弹塑性分析，欧文曾建议将裂纹尖端的塑性区也视为裂纹体的一部分，即用塑性区尺寸ry对实际的裂纹长度ap进行修正，将修正后的裂纹尺寸视为有效裂纹尺寸aeff。其计算公式为
aeff=ap+ry （13-10）
显然，这种修正办法，只对于小尺寸塑性区情况才认为是可接受的，此时，应力强度因子也需做相应的修正。