8.3.2 扭转试验的原理
扭转试验是对圆柱形（或管形）试样施加扭矩T（使试样两端承受大小相等、方向相反、作用面垂直于试样轴线的力偶），测量扭矩T及相应的扭角θ，试验一般扭转至断裂，以便测定金属材料的各项扭转力学性能指标。如把扭矩T及相应的扭角θ绘制成曲线，即得到T-θ扭转图。
当试样承受扭矩T时，试样表面的应力状态如图8-23所示。在与试样轴线呈45°的两个斜截面上承受最大与最小正应力σ1及σ3，在与试样轴线平行和垂直的截面上承受最大切应力τ，两者比值近于1。在弹性变形阶段，试样横截面上的切应力和切应变沿半径方向的分布是线性的，如图8-24a所示。当表层产生塑性变形后，切应变的分布仍保持线性关系，但切应力则因塑性变形而有所降低，不再呈线性分布，如图8-24b所示。
1.扭转时的切应力
圆柱体试样扭转时，平衡外加扭矩T是由横截面上无数的微剪切力组成的。
如图8-25所示，设距圆心ρ处的切应力为τρ，此处的微面积dA上的微剪切力为τρdA。则有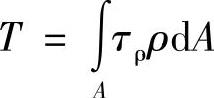
，弹性范围内，切应力沿半径成正比，表面切应力最大，即
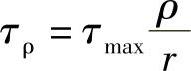，故，
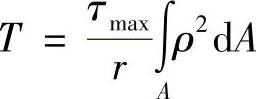
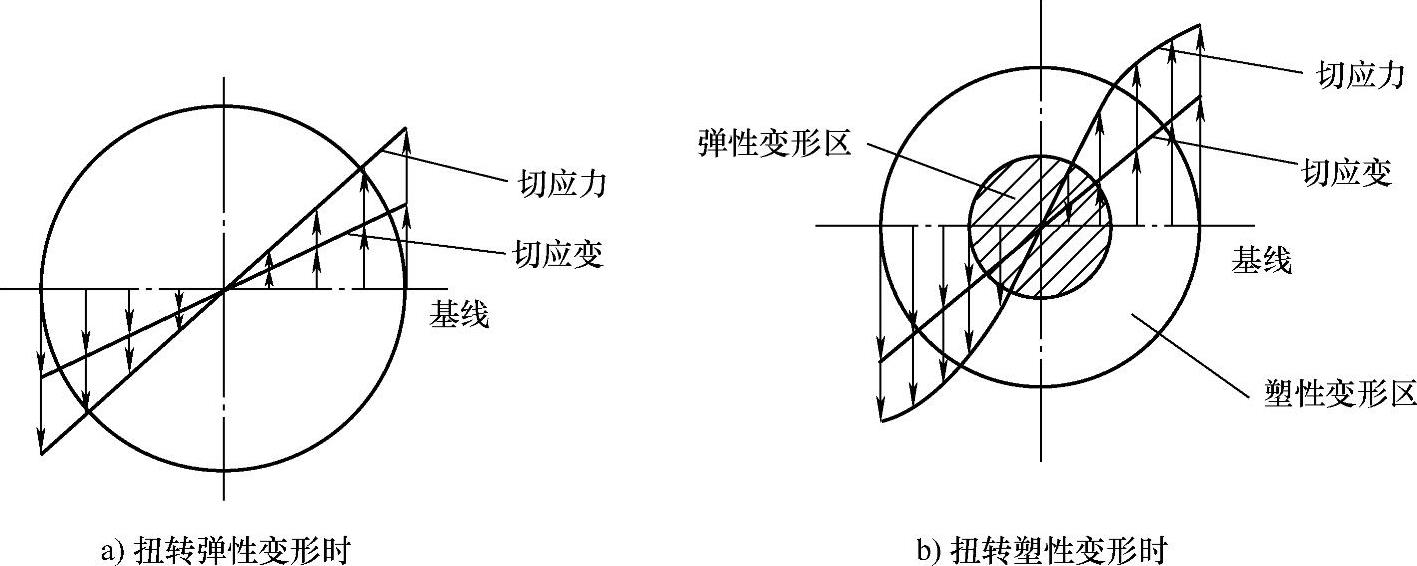
图8-24 扭转弹性变形横截面切应力和切应变分布
令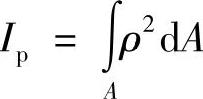
，这是仅与横截面的形状和尺寸有关的几何量，称为试样横截面对形心的极惯性矩，则有
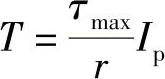，令W=Ip/r，即扭转横截面系数，则有
τmax=T/W （8-36）
对于实心圆截面
Ip=πd4/32，Wp=πd3/16
对于空心圆截面
Ip=π（d4-d41）/32，Wp=πd3（1-d41/d4）/16
式中 d——空心圆外径；
d1——空心圆内径。
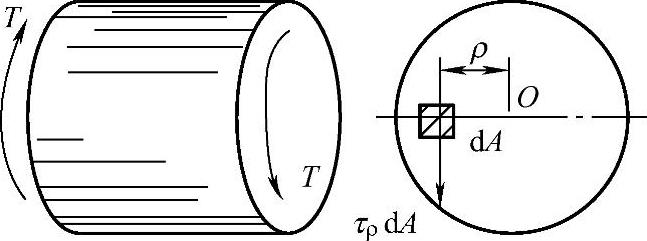
图8-25 圆柱体试样扭转时的切应力计算示意图
2.扭转时的切应变
当直径为d、长度为Lc的圆柱体两端的相对扭转角为θ时，试样表面的切应变γ为
γ=rθ/Lc=dθ/（2Lc） （8-37）
3.剪切弹性模量
剪切弹性模量G的计算公式为
G=τ/γ=TLc/（θIp） （8-38）
1）当切应力使试样表面发生塑性变形时，圆柱体横截面上的切应力τρ与该点到轴线的距离ρ失去比例关系，如图8-24b所示。由材料力学可知：扭转试验时，距离圆柱体轴线为ρ处，切应变γρ=ρdθ/dx=ρθ，切应力τρ=（3T+θdT/dθ）/2πρ3；在试样表面（ρ=d/2处），τ=4（3T+θdT/dθ）/πd3，其中，dT/dθ为T-θ曲线上试验点的斜率。
2）薄壁管扭转时的切应力。当薄壁管的壁厚α0远小于其平均半径rm时[rm=（d+d1）/2，α0/rm＜10]，可以认为试样横截面上沿壁厚方向切应力近似相等，它们对试样轴线的力矩与外加扭矩T平衡，因此平衡方程为T-2πrmα0τrm=0，所以薄壁管扭转时的切应力
τ=T/（2πr2mα0） （8-39）
在薄壁管扭转时的切应力公式推导中没有应用胡克定律，式（8-39）可应用于整个扭转试验过程，即此式（8-39）不仅可用于薄壁管扭转弹性变形阶段，也可用于薄壁管扭转塑性变形阶段。