5.7.1 弹性模量的测定
1.图解法测定拉伸弹性模量
拉伸试验时,用记录仪器记录轴向力-轴向变形曲线,如图5-21所示。绘制曲线时,力轴比例的选择应使轴向力-轴向变形曲线的弹性直线段的高度超过力轴量程的3/5以上。变形放大倍数的选择应使轴向力-轴向变形曲线的弹性直线段与力轴的夹角不小于40°为宜。根据拉伸曲线图选定弹性直线段,在直线段选取相距尽量远的A、B两点之间的轴向力增量和相对应的变形增量。然后,按照式(5-23)计算拉伸弹性模量E,即
E=(ΔF/So)/(Δl/Lel) (5-23)
式中 ΔF——A、B两点之间的力值增量(kN);
So——试样的原始截面积(mm2);
Δl——A、B两点之间的引伸计轴向变形增量(mm);
Lel——轴向引伸计标距(mm)。
可以借助于直尺将弹性直线段延长,在相距较远的两点之间读取轴向力增量和相应的轴向变形增量。
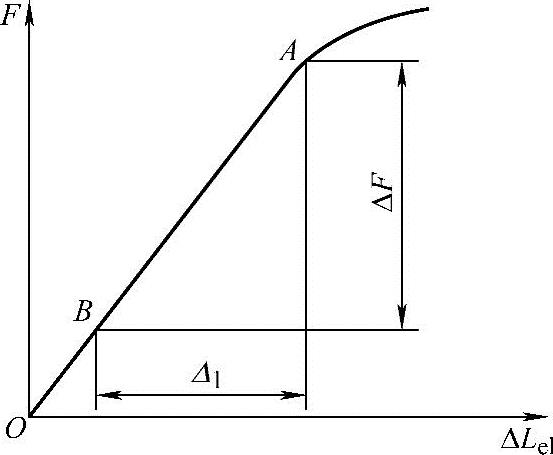
图5-21 图解法测定拉伸弹性模量
注意:当用应变片来测定变形时,记录的力-变形曲线中,横坐标的量纲为应变,它等于(ΔL/Le)。
2.逐级加载法测定拉伸弹性模量E
逐级加载法测定拉伸弹性模量时,不需要记录力-变形曲线,只要求用精度高的引伸计。试验时,在弹性范围至少读取8对轴向力和相应的轴向变形数据对。然后,按线性回归方法(最小二乘法)计算拉伸弹性模量。下面以实例来说明。读取的原始数据对见表5-11,所用试样的直径为10mm,引伸计标距为50mm。
由表5-11可知:1~7数据对之间的增量关系是线性的,超过8及以后的数据呈非线性比例关系的变化。因此,在计算拉伸弹性模量时,只能采用8及以下的数据对。将上述8对数据对转换成应力-应变数据对,用最小二乘法进行直线拟合,并求出直线的斜率,此斜率即为拉伸弹性模量E。其计算公式为
E=[k∑(eR)-∑e∑R]/[k∑e2-(∑e)2] (5-24)(https://www.daowen.com)
式中 e——Δl/Lel;
R——F/So;
k——数据对数目。
按式(5-24)计算可得到
E=213GPa
表5-11 钢的拉伸弹性模量测定记录
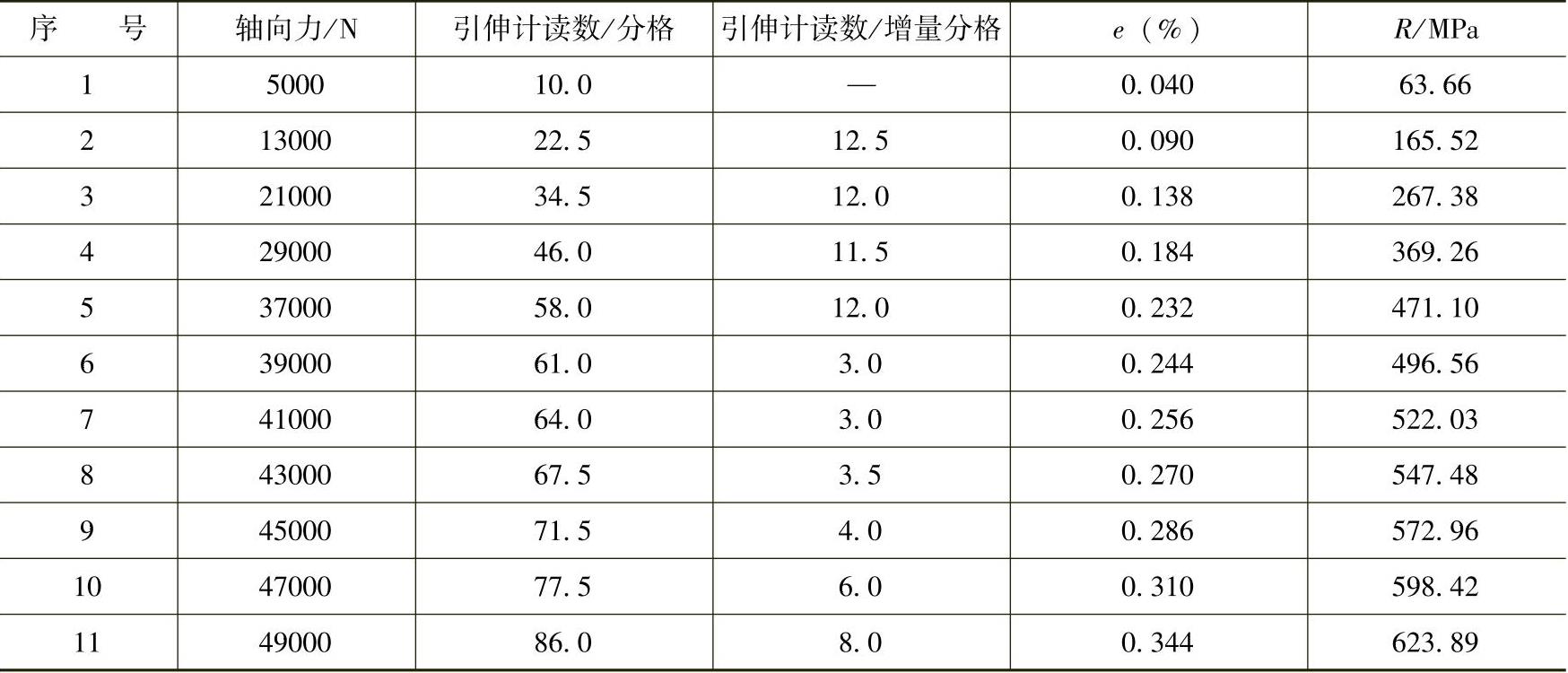
注:引伸计读数的每分格值为0.002mm。
3.图解法测定切线模量Etan和弦线模量Ech
在记录的轴向力-轴向变形曲线上,根据规定的应力或应变取R点,并通过该点作切线,在相距尽量远的A、B两点读取轴向力增量和相应的轴向变形增量,如图5-22所示,然后按式(5-25)计算切线模量。类似地,根据规定的轴向应力或轴向应变取A、B两点,在轴向力-轴向变形曲线上,读取轴向力增量和相应的轴向变形增量,如图5-23所示,然后按式(5-26)计算弦线模量。两种图解法的图形要求为:力轴比例的选择应使轴向力-轴向变形曲线的弹性直线段的高度超过力轴量程的3/5以上。变形放大倍数的选择应使轴向力-轴向变形曲线的弹性直线段与力轴的夹角不小于40°为宜。
Etan=(ΔF/So)/(Δl/Lel) (5-25)
Ech=(ΔF/So)/(Δl/Lel) (5-26)
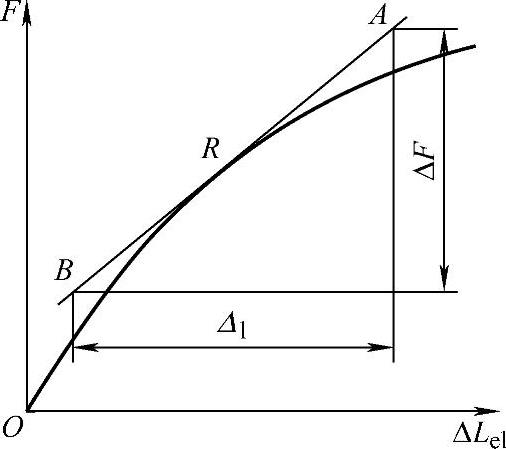
图5-22 图解法测定切线模量
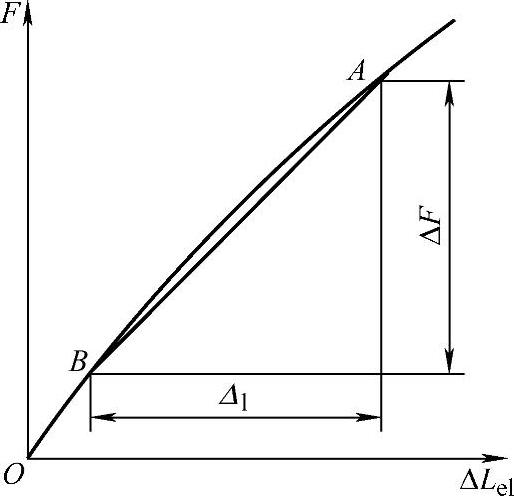
图5-23 图解法测定弦线模量
