∗13.1.5 裂纹扩展能量释放率GⅠ
线弹性断裂力学处理带裂纹体的问题有两种方法：一种是上面所讨论的应力场分析法；另一种是能量分析法，这就是本节所要讨论的问题。
根据热力学定律，自然界一切过程的进行必须遵守能量守恒原理，而且一切自发进行的过程，一定使系统本身的能量降低。裂纹失稳扩展是一个自发进行的过程，只要分析裂纹扩展过程中的能量变化，建立平衡方程，就可以获得裂纹失稳扩展时的能量判据。这种分析方法较为直观，能更清楚地揭示断裂韧度的物理意义。
1.GⅠ的物理意义
我们首先来讨论格里菲斯（Griffith）理论。该理论从材料中存在宏观裂纹这一事实出发，根据能量平衡条件，成功地说明了材料实际强度与裂纹尺寸之间的关系。
格里菲斯公式的数学表达式为
式中 E——弹性模量；
γ——表面能。
由式（13-18）可知，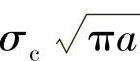
也可作为评定材料脆性断裂的力学性能指标。
上述能量分析法也可以这样来解释：裂纹扩展单位面积时，系统所提供的弹性能量∂U/∂A是推动裂纹扩展的动力，其所需要提供的能量为裂纹扩展阻力。通常把裂纹扩展单位面积由系统所提供的弹性能量叫作裂纹扩展力，或称为裂纹扩展时的能量释放率，简称能量释放率，以GⅠ表示（Ⅰ表示Ⅰ型裂纹扩展）。G与外加应力、试样尺寸和裂纹尺寸有关。在格里菲斯裂纹体中，其值为
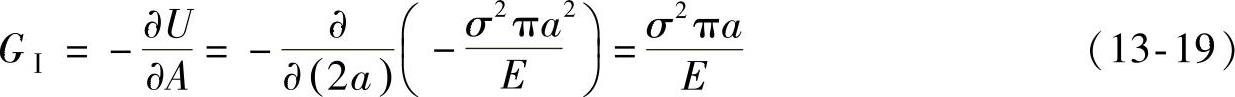
在临界状态下的裂纹扩展能量释放率记作Gc（表示平面应力状态下的断裂韧性），其值为
由式（13-20）可知，临界状态下的裂纹扩展能量释放率数值上等于临界裂纹扩展阻力。Gc越大，材料抵抗裂纹扩展的能力也越大，故Gc是材料抵抗裂纹失稳扩展的度量，也叫作材料的断裂韧性。
实际上，对金属材料来说，裂纹扩展时裂纹前端不可避免地要产生塑性变形，因而裂纹扩展时释放的弹性能不仅要支付表面能增加，而且要支付屈服区的塑性变形功Up，而且Up往往大于γ，故式（13-20）中的γ应改为（γ+Up），即
Gc=2（γ+Up） （13-21）
2.应力强度因子KⅠ与能量释放率GⅠ的关系
假设一无限宽板上有长为2a的穿透裂纹，在裂纹远处受均匀拉伸正应力σ的作用。根据线弹性断裂力学理论计算，这个穿透裂纹尖端的应力场强度因子为
对于这种裂纹，根据能量分析，其能量释放率GⅠ为
对比式（13-22）与式（13-23）可知，在平面应力情况下
在平面应变情况下
上述公式是根据带裂纹的无限宽板这种特定情况下推导出来的。对于一般的含裂纹体，根据弹性理论也可以推导出上述结果。
在裂纹失稳的临界状态下有
对于某一给定材料，裂纹的表面能和失稳扩展时所消耗的塑性变形功Up都是材料常数，与裂纹大小、形状及外载情况无关，所以GⅠc是材料本身的固有性能。
由上述分析可知，要使裂纹失稳扩展，必须使裂纹扩展力GⅠ大于或等于临界点的阻力GⅠc，即
GⅠ≥GⅠc （13-28）
这就是断裂判据，满足上述方程，构件即发生失稳断裂。