12.4.2 试验数据的处理
2026年01月15日
12.4.2 试验数据的处理
大量试验证明,Δεe/2-2Nf、Δεp/2-2Nf、Δσe/2-2Nf、Δσ-Δεp/2在双对数坐标上呈直线关系,通过一元回归分析可建立起它们的函数关系式,从而获得应变疲劳性能的六大参量。
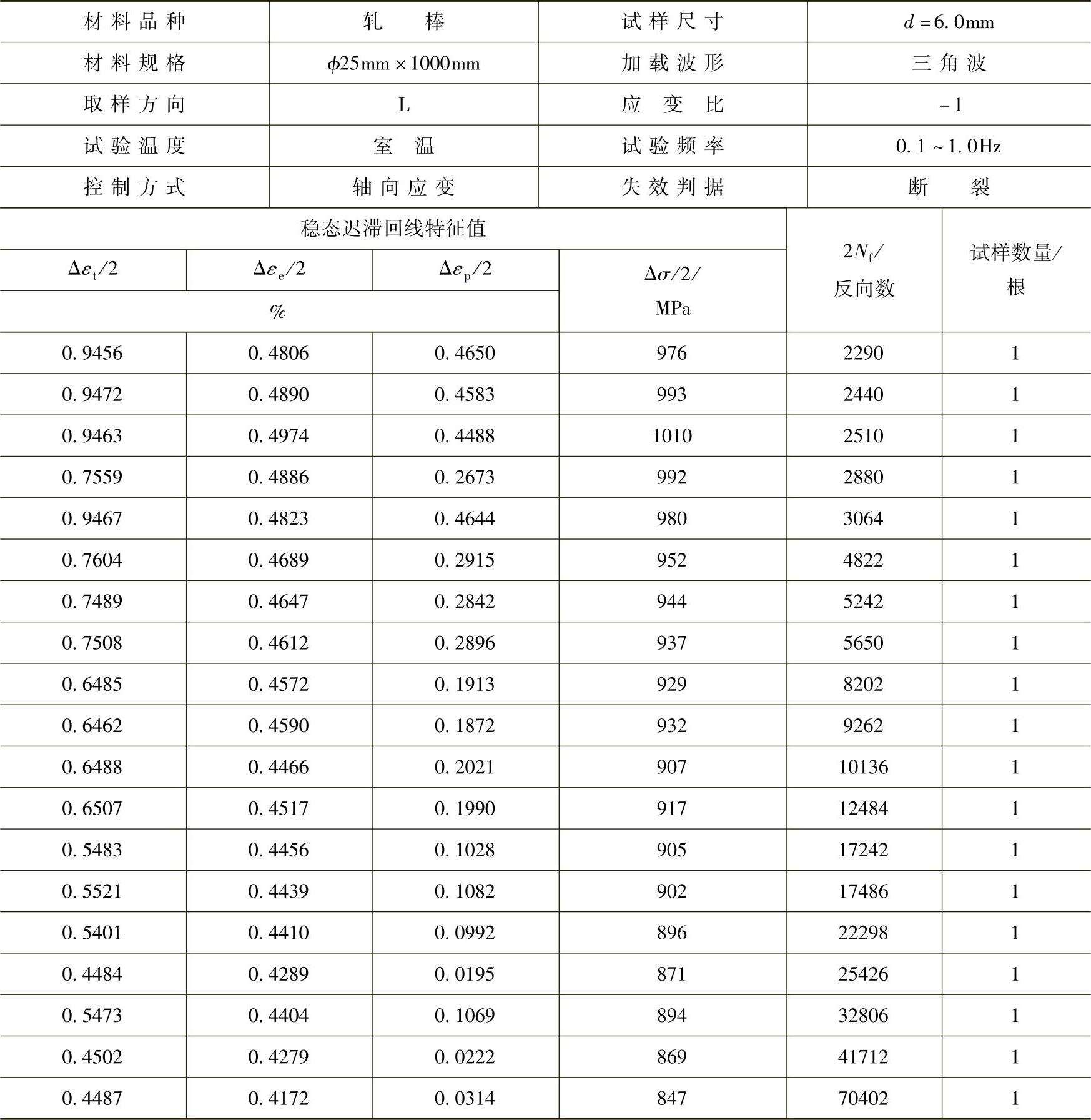
表12-1 合金钢低周疲劳试验数据的获得
取xi=lg(2Nf)i,yi=lg(Δεe)i,按最小二乘法得到Δεe/2-2Nf的对数线性方程,其一般形式为

式中i=1,2,3,…,n,n是试验观测值个数。
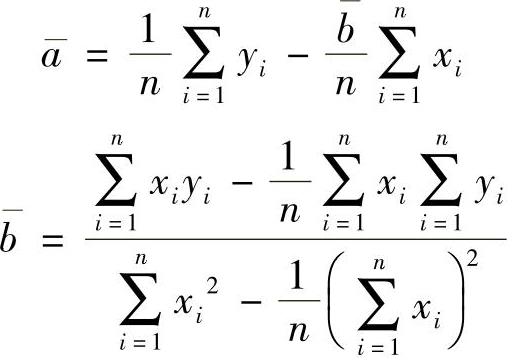 (https://www.daowen.com)
(https://www.daowen.com)
令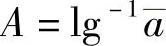 ,A值即为σf′,
,A值即为σf′,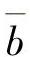 值为疲劳强度指数b。
值为疲劳强度指数b。
若取xi=lg(2Nf)i,yi=lg(Δσ/2)i,同理可得A值为疲劳强度系数σf′,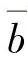 值为疲劳强度指数b。
值为疲劳强度指数b。
若取xi=lg(2Nf)i,yi=lg(Δεp)i,同理可得A值为疲劳延性系数εf′,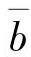 值为疲劳延性指数c。
值为疲劳延性指数c。
若取xi=lg(Δεp)i,yi=lg(Δσ)i,同理可得A值为循环强度系数K′,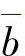 值为循环强度指数n′。
值为循环强度指数n′。
线性方程的线性相关程度,可用相关系数R检验(请参见本书附录K)。

式中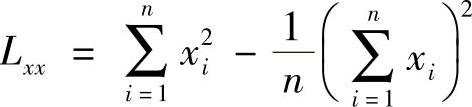 ,
,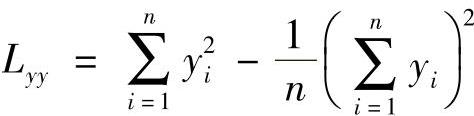 ,
,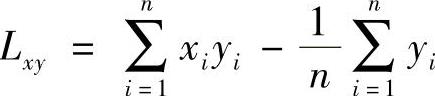 。
。
根据观测值个数n查相关系数检验表(见本书附录K),当计算出的R值大于与n-2相对应的R起码值时,即为线性相关。
