15.3.1 快速傅里叶变换
傅里叶变换是一种将时域信号变换为频域信号的积分变换形式。在频域分析中,信号的频率及对应的幅值、相位(统称为频谱)反映了系统的性能。快速傅里叶变换(Fast Fou-rier Transform,FFT)是离散傅里叶变换(Discrete Fourier Transform,DFT)的快速实现方法,是数字信号处理(DSP)中的重要算法之一。
1.快速傅里叶变换的基本原理
非周期连续时间信号x(t)的傅里叶变换为

上式计算出来的是信号x(t)的连续频谱。实际系统中经常得到的是信号x(t)的离散采样值x(nT)(T为采样周期,n=0,1,…,N-1),简记为x(n)。N点采样值频谱取样的谱间距为
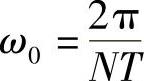
那么序列x(n)的离散傅里叶变换为
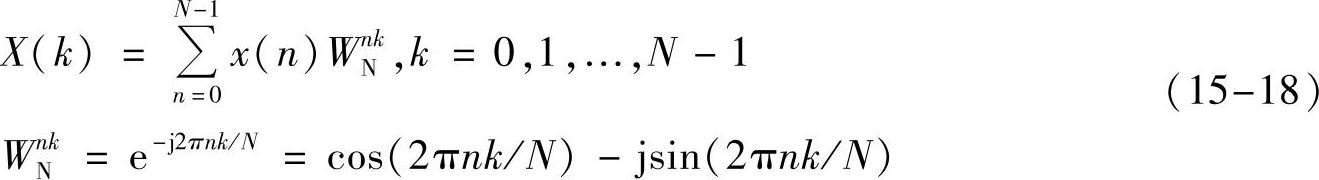
式中,X(k)是时间序列x(n)的频谱;WN称为蝶形因子或旋转因子。对于N点时域采样值,经过离散傅里叶变换计算,可以得到N个频谱条。每计算一个X(k)值需要N次复数相乘和N-1次复数相加,对于N个X(k)应重复计算N次。离散傅里叶变换共需要计算N2次复数乘法和N(N-1)复数次加法,在N较大(例如N=1024)时,这个计算量很大,为此需要采用快速离散傅里叶变换。
序列x(n)按序号n的奇偶可以分成两组,即
x1(n)=x(2n)
x2(n)=x(2n+1),n=0,1,…,N/2-1
所以,x(n)的离散傅里叶变换可写为
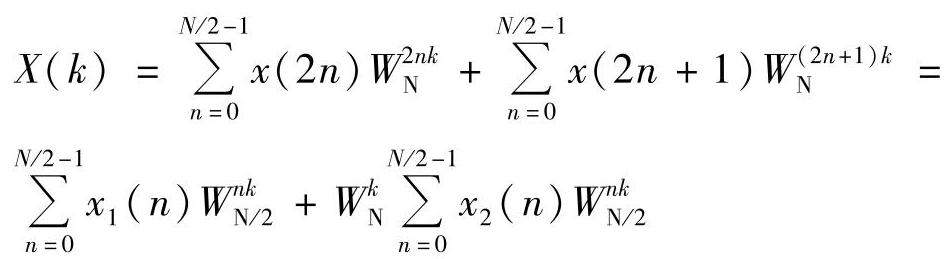
由此可得
X(k)=X1(k)+WkNX2(k),k=0,1,…,N/2-1 (15-19)(https://www.daowen.com)
式中
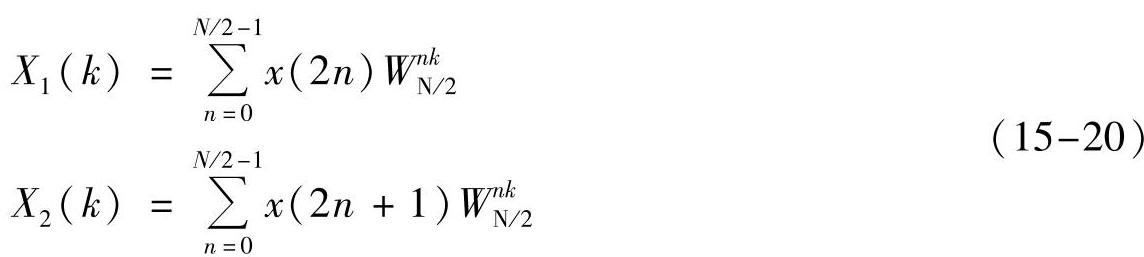
X1(k)和X2(k)分别是x1(n)和x2(n)的N/2点DFT。上面的推导表明,一个N点的DFT可以分解为两个N/2点的DFT,而这两个N/2点的DFT又可以合成一个N点的DFT,但上面给出的公式仅能得到X(k)的前N/2点的值,要用X1(k)和X2(k)来表示X(k)的后半部分,还必须运用蝶形因子WN的周期性与对称性,即
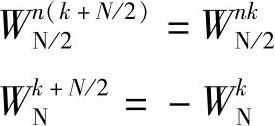
因此,X(k)的后N/2点可以表示为
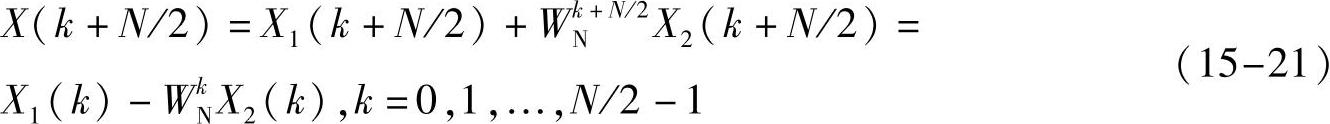
由此可见,一个N点的DFT可以分解为两个N/2点的DFT,每个N/2点的DFT又可以分解为两个N/4点的DFT。依此类推,当N为2的整数次幂(N=2M)时,由于每分解一次降低一次幂阶,所以通过M次分解,最后全部成为一系列2点DFT运算。这样计算量可以减为(N/2)log2N个乘法运算和Nlog2N个加法运算,比DFT的计算量大大减轻。以上就是按时间抽取的FFT算法。式(15-19)和(15-21)表示的运算称为蝶形运算。
2.FFT的实现
例15-1 时间抽取的FFT算法DSPC语言实现实例。
FFT运算函数与主函数为


由于上述代码中调用了pow、log、cos及sin函数,该函数所在的C文件应包含头文件math.h。调用FFT函数进行FFT运算时,需要提供的参数为FFT运算点数、时域序列的实部与虚部。另外,FFT函数包含的函数finv(N,Xr,Xi)为倒序运算,函数代码如下。
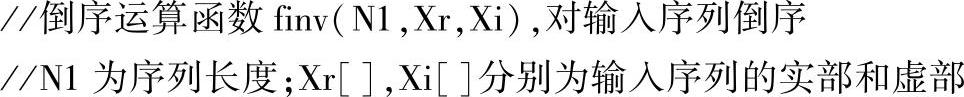

可以通过CCS软件调试该程序,并用其中的View>Graph>Time/Frequency菜单功能,显示变量INPUT与DATA图形,观察FFT的效果。
