2.4.2 水资源系统—生态系统—社会系统的演化与约束机理分析
水资源系统、生态系统和社会系统之间既是竞争的又是互补的，它们间的协调演化过程既是通过其界门的协调得以延续，又是通过界壁的约束作用得以存在。我们以界壳交换率为变量，列出Lotka-Volterra方程（称为界壳交换率方程），来描述协调演化过程，它可以反映出3个系统的演化状态、可持续发展、竞争互补于一体的既有横向联合又有竞争协调的机制。
基于界壳交换率的Lotka-Volterra方程：
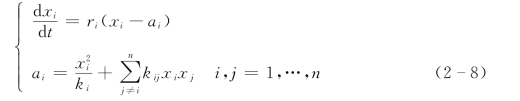
式中：xi为第i个系统与外界的界壳交换率，是第i个系统开放程度的标志，0≤xi≤1；ki为第i个系统的内部协调程度，0≤ki≤1；kij为第j个系统对第i个系统的影响，反映竞争关系，0≤kij≤1；ri为第i个系统的发展程度，0≤ri≤1；ai为第i个系统的自身衰减和交互内耗部分。
将方程（2-8）写成矩阵形式：
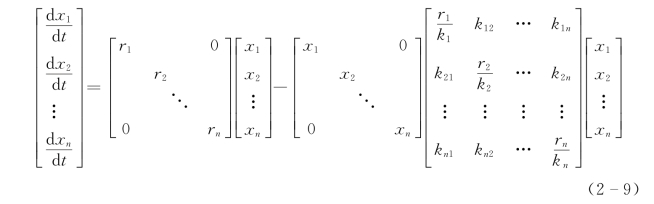
即：
则方程（2-8）的不动点为
，得
，亦即：
讨论：
（1）
，稳定（僵化）不动点。表明各系统与外界的界壳交换率恒定不变，彼此间的交换程度不受天然来水量和耗水量变化的影响，系统间缺乏有效的协调，水资源的调控效率较低，难以协调和保持各系统的可持续发展。
（2）
，即
，不稳定的不动点。表明各系统与外界的界壳交换率加强，意味着依据各系统自身发展和与外界协调性来合理调控、有效利用水资源。既强调各系统的自身发展（内部挖潜），又充分考虑各系统间的协调影响，水资源的调控效率较高，能较好地协调和保持各系统的可持续发展。
（3）
，即
，不稳定的不动点。表明各系统与外界的界壳交换率减弱，各系统内部水资源利用率低下，与外界协调不够，调控策略存在着方向性问题。
随着天然来水量的变化、生态环境的演化以及社会经济的不断发展，其对水资源的需求份额和需求层次以及政策导向等因素的变化，各系统间的界壳交换率也将随之产生变化。设上述影响因素分别为y1，y2，…，ym，对应的影响程度（可正可负）分别为c11，c12，…，cnm，则各系统的界壳交换率方程（2-8）可改写为：
其不动点方程为：
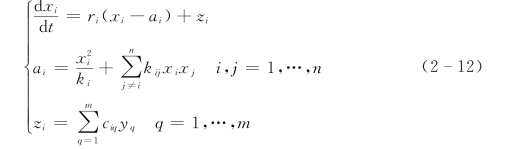
经过适当的矩阵变换有：
其不动点方程变为：
亦即
，从而有：
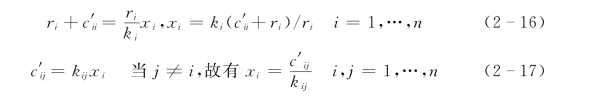
由此可见，若yg的变化是随机的，不动点就是不稳定的。也就是说，在CY的变化影响下，需要加强各系统间的协调系数kij和系统内的协调系数ki，才能维持各系统的协同发展。
由于ki是时间的函数，即ki（t），且ki（t）与xi（t）成正比，表明系统内部的协调会促进系统与外界界壳交换率的提高；反之界壳交换率的增大会加快系统内部的协调进程。这种作用的大小还受制于
表达了负反馈或限制作用使dxi/dt变小。
对城市水资源系统、社会经济系统和生态环境系统而言，研究各竞争的系统在不同的内部协调能力ki（t）下，如何竞争有序；又如何在天然来水量的变化情况下，求得各系统的共存和协调发展，寻求各系统的竞争发展轨迹是水资源调控研究的目标。城市水资源系统、社会经济系统和生态环境系统除竞争共存外，还有其内涵，即协同演化。也就是说在界壳交换率方程中的某一竞争关系kij变为负或ri变为负，那么它的物理意义又从系统j向系统i争夺资源转变为促进系统i的发展，或者说它们的演化从竞争转变为依托，亦即协同演化。在界壳交换率方程中，ri（xi-∑kijxixj）和ri的可正可负，共同构成了各种非线性的界门开关速度，控制着水资源系统、社会经济系统和生态环境系统的演化发展。
基于界壳交换率的Lotka-Volterra方程——界壳交换率方程，其重要性不仅因为它可以反映出3个系统的演化状态、可持续发展、竞争互补于一体的既有横向联合又有竞争协调机制，而且它作为一类典型的非线性动力学模型，在水资源系统的理论研究中将具有非常重要的研究价值。对界壳交换率方程的动力学性质研究，我们最关心的是各个系统变量随时间演化的长期动力学行为：是否每个都最终演化到一个极限值（即所谓全局渐进稳定性问题）或演化到一个不变集（与稳定性及约化问题有关）？什么条件下系统的某些系统变量会趋近于零（与持久性问题相关）？在什么条件下存在周期、概周期解（与共存问题相关）甚至混沌解等？这些都有待进一步深入研究。