3.9.5 应用实例
本节以某城市需水预测为例,采用vensim软件进行模拟计算。城市需水量预测仿真模型如图3-12所示。
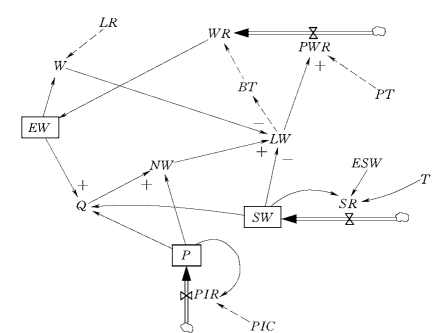
图3-12 城市需水量预测仿真模型混合图
3.9.5.1 模型的建立
1.参数指标
EW——城市供水总量;
SW——节水量;
P——用水人口;
PWR——供水总量规划增加率;
SR——节水率;
PIR——人口增长率;
WR——供水总量实际增加率;
BT——建设时间;
W——城市实际供水总量;
LW——供水紧张程度城市缺水量;
NW——城市需水量;
Q——人均综合用水定额;
PT——规划时间;
LR——管网漏失率;
ESW——期望节水量;
T——实施时间;
PIC——人口增长系数;
ΔW——每年通过建设增加的城市供水量。
其中,EW、SW、P为状态变量;PWR、SR、PIR为速率变量;WR、BT、W、LW、NW、Q为辅助变量;PT、LR、ESW、T、PIC为常量。
2.建立方程
PWR=LW/PT
WR=DELAY3(PWR,BT)
BT=LW/ΔW
EW=INTEG(WR),W=EW*(1-LR)(https://www.daowen.com)
Q=(EW+SW)/P
NW=Q*P
P=INTEG(PIR)
PIR=PIC*P
SW=INTEG(SR)
SR=(ESW-SW)/T
LW=NW-W-SW
3.已知数据
LR=0.09,PIC=0.0192
T=10a,PT=10a
ESW=4.5e+008,ΔW=1.825e+007
EW初始值=4.12669e+009
P初始值=7.949e+006
SW初始值=1.58052e+008
3.9.5.2 模型求解
使用建模软件vensim绘制城市需水量仿真模型混合图,写入方程进行计算,可得出结果,如图3-13所示。
运用模型对该市需水量进行预测,以2000年为初始年,预测2010年,由图3-13可得具体结果见表3-20。
表3-20 预测结果
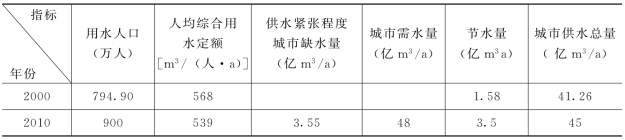
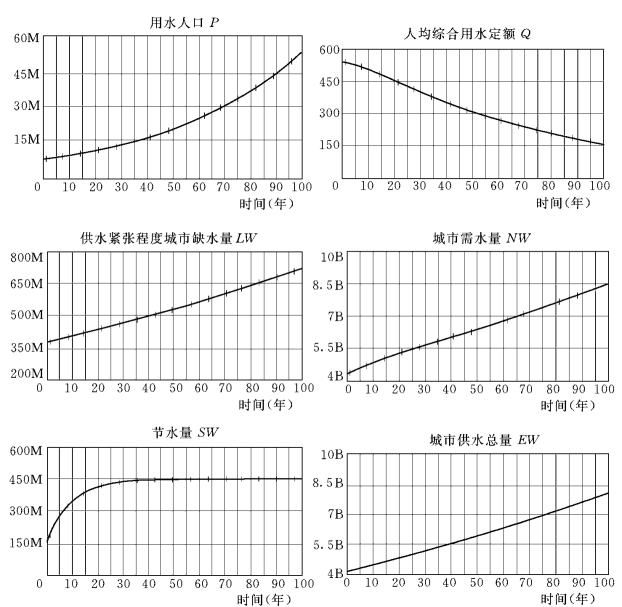
图3-13 vensim软件模拟仿真结果
3.9.5.3 模型检验
1.模型的合理、有效性检验
将模型用计算机语言表达,上机运行,用vensim软件提供的编译检错及跟踪功能检验模型表达的正确性,根据运行结果判断模型的合理性。
2.结构和参数灵敏度检验
变化模型方程和模型的参数值,通过结果得知,这种变化对于模型的行为影响很小,且在特定干扰和随机干扰下,系统都能实现特定的目标,故模型的结构和参数灵敏度得以检验。
3.方程式极端条件检验
对模型中各个方程式在其变量的可能变化的极端条件下进行检验,特别是对速率方程严格进行极端条件检验,来了解模型的非线性特性并揭露模型中的弱点。通过检验,发现模型中各方程仍然有意义。
