3.7.2　最小二乘支持向量机

3.7.2　最小二乘支持向量机

最小二乘支持向量机（LSSVM）是支持向量机的一种，它是将标准支持向量机算法中的不等式约束转化为等式约束而得到的。对非线性回归问题，设训练样本为：

非线性回归函数为：

对于最小二乘支持向量机，优化问题变为：

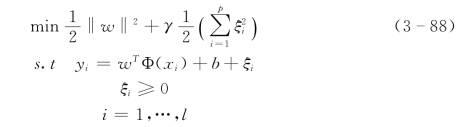
求解式（3-88）的优化问题，可以引入Lagrange函数：

式中：αi为Lagrange乘子；常数γ>0，它控制对超出误差的样本的惩罚程度。

最优的αi和b可以根据KKT（Karush-Kuhn-Tucker）条件得到：

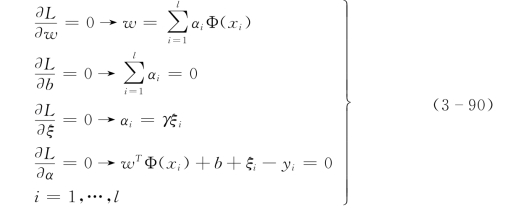
由式（3-90），优化问题转化为求解如下的线性方程：

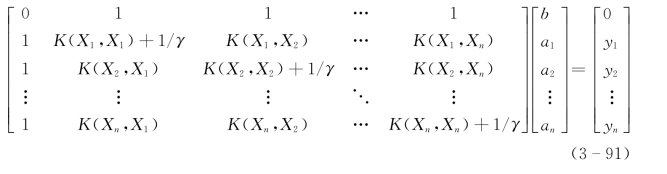
其中，K（xi，xj）为核函数。

从而得到非线性回归函数的解为：

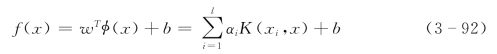
由于γ>0为一常数，不论误差的大小，它对超出误差的样本的惩罚程度是不变的。这样对超出误差的极端样本（较大的和较小的样本）的惩罚力度较弱，使得训练精度和推广能力的改善能力欠佳。