3.3.3 移动平均法(确定型)
采用移动平均法进行预测,就是不断的引进现象或过程发生的新的实际统计数据,加以移动平均,将其平均数作为预测值。
移动平均的目的在于消除原序列的偶然因素的影响,使样本值得到修匀,用于推算未来事务的发展变化。采用这种方法的假定条件是现象的发展变化与近期若干期实际数据有关,而与较远时期的实际数据值联系不大。其主要适用于对变动不大的、发展趋势比较稳定的水平年型的水资源需求进行短期预测。
1.一次移动平均法
一次移动平均法又称简单移动平均法,就是在算术平均法的基础上,通过逐步分段移动求得下一期的预测值。
一次移动平均值计算公式如下:
![]()
式中:Mt为第t期的一次移动平均值(作预测时可作为t+1期的预测值);Xt为第t期的样本值;N为移动平均的样本个数(即移动平均的时段长)。则第t+1期的预测值取为X∧=M(1)t(N),且移动项数N的大小对预测值影响较大,选取带有一定的经验性。
2.二次移动平均法
二次移动平均就是在一次移动平均值的基础上再做一次移动平均。第二次移动平均并不直接用来预测,而是为了求出平滑系数,建立移动预测模型,以便克服第一次移动平均值的滞后现象。
二次移动平均值计算公式如下:
![]()
式中:M(2)t为第t期二次移动平均值。
二次移动平均法预测的基本公式:
![]()
式中:t为当前的时期数;T为由t至预测期的时期数,T=1,2,…;at、bt为平滑系数;at为截距,![]() 为斜率,
为斜率,![]() 。
。
在应用二次移动平均法进行水资源需求预测时,应该注意以下两点。
(1)已知时间序列数据点的分布应呈直线趋势,否则不宜采用。
(2)计算第二次移动平均数的样本数(即移动平均的时段长)应与第一次移动平均时取相同个数。
3.算例
已知黄河流域1971~1986年需水资料,见表3-4,根据移动平均法预测1987年的需水量。
表3-4 1971~1986年的需水资料 单位:亿m3
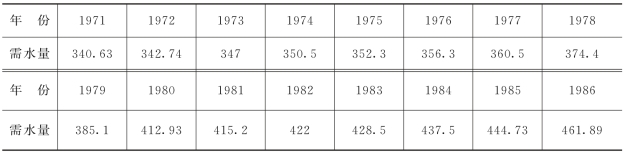 (https://www.daowen.com)
(https://www.daowen.com)
计算方法及步骤如下。
(1)计算一次移动平均值![]() 。
。
假设N=5,根据公式(3-20),得:
![]()
并作为下一期![]() 的一次移动平均值,同样可得
的一次移动平均值,同样可得![]() 等,计算结果见表3-5中的第(3)列。
等,计算结果见表3-5中的第(3)列。
(2)计算二次移动平均值![]() 。
。
为保持一致也取N=5,根据公式(3-16),则:
![]()
作为下一期![]() 的二次移动平均值,同样可得
的二次移动平均值,同样可得![]() 等,计算结果见表3-5中的第(4)列。
等,计算结果见表3-5中的第(4)列。
(3)计算平滑系数at,bt。
根据公式,![]() 分别计算平滑系数,那么:
分别计算平滑系数,那么:
![]()
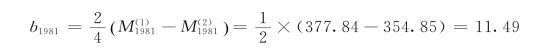
同样可得a1982,a1983等,计算结果见表3-5中的第(6)、第(7)列。
表3-5 计算成果 单位:亿m3
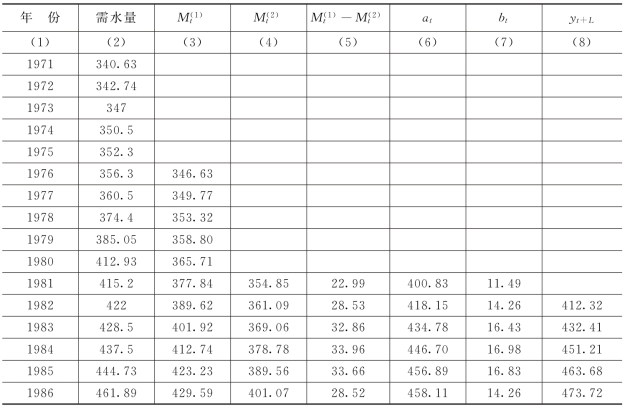
(4)计算预测值yt+T。
根据公式(3-17),计算出预测值见表(3-5)中的第(8)列。
以1986年为基期,a1986=458.11,b1986=14.26,建立1986年起的趋势直线:
y1986+L=a1986+b1986T
y1987=458.11+14.26×1=472.37(亿m3)
与实际用水值479.31亿相差1.45%,预测效果较好。
