11.4.2 风险计算方法
风险计算常用的方法有基于概率论和数理统计的方法、重现期法、蒙特卡洛模拟(MC)法和JC法,此外还有模糊风险分析计算法、灰色风险分析计算法、极大熵风险分析方法等。
11.4.2.1 基于概率论和数理统计方法
(1)直接积分法。
影响风险主体的不确定性风险变量若服从一些典型的概率分布,如三角形分布、威布尔分布、正态分布、皮尔逊Ⅲ型分布等,利用概率分布密度函数的积分便可分析计算可靠率或风险率指标。
当风险变量为一维随机变量x时,其概率分布密度函数为f(x),在决策目标是极大化情况下,决策指标不小于某一规定值x0的风险率为:


11.4.2.2 重现期法
这是从工程水文设计角度提出的风险率计算方法,基于两个前提假设:
(1)设计水文事件在年际间的发生是独立不相关的。
(2)设计水文事件在各年的发生概率相等。
若工程设计重现期为T年,工程的荷载为L,抗力为R,则1年内工程发生失事的风险率用公式表示如下:
![]()
N年内发生失事的风险率为:
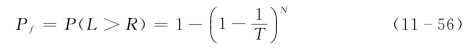
重现期方法在计算风险上具有简单易行的优点,但有其局限性:一是重现期是由历史资料的统计和外延推得的,因此,风险的精度受统计资料的限制;二是因为仅考虑水文风险因素,导致工程风险率计算结果偏小。
11.4.2.3 蒙特卡洛模拟法
在水资源系统中有时各风险变量之间存在着比较复杂的影响机制,不容易确切估计和确定分布线型与参数,不容易集中考虑各种变量的相关影响,而用模拟的方法进行复杂水资源系统的风险分析是一种行之有效的方法。蒙特卡洛模拟是用一随机数发生器产生具有相同发生概率随机数,将其输入模型进行模拟试验,经过反复多次试验,得出风险变量的频率分布,通过统计分析可得风险指标。
不论是概率论方法,还是蒙特卡洛法,风险因素概率分布或概率分布密度函数的确定是两种方法能够使用的关键问题,但是有些风险因素由于资料少,不能用统计的方法确定其概率分布,只能主观给出,通常主观估计的概率分布有三角形分布和梯形分布两种形式。以下给出常用的几种分布的随机模拟公式:
(1)正态分布模拟。
在得到[0,1]之间均匀分布的伪随机数后,通过两种方法能得到正态分布的随机序列:一种是变换法;另一种是随机数和法。



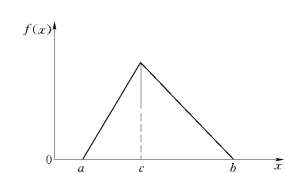
图11-4 三角形分布密度函数
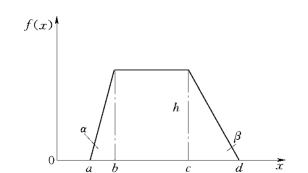
图11-5 梯形分布密度函数

Step1-确定输入变量(主要风险因素)及其概率分布。
Step2-通过模拟试验,独立地随机抽取各输入变量的值,并使所抽取的随机数值符合既定的概率分布(具体分布由实际问题确定)。
Step3-按照风险目标与主要风险因素之间的函数关系,计算输出变量。
Step4-重复Step2、3,直到模拟次数满足预定的精度要求,以频率统计的方法计算出风险率。
11.4.2.4 界壳的泛系观控法
界壳论是关于系统周界的一般理论,是专门研究称为界壳的系统周界,认为系统以它的周界(系统边界)与环境相分离,无论从系统向环境,或是从环境向系统的物质、能量、信息的传输,都必须经过这一周界,这样,系统周界对系统的形成与发展,对系统状态的变化都起着重要作用,乃至决定性的作用。
泛系观控是泛系理论的重要组成部分。泛系观控理论认为时间、空间、物质、能量和信息科学五基元都不能独立存在,而唯有作为泛系的“时间—空间—物质—能量—信息”方能独立存在。将界壳论与泛系观控有机地结合起来,建立起界壳的充分可观控的泛系观控模型,结合泛系风险观控分析技术,该模型便可应用于复杂水资源调控的风险分析问题。(https://www.daowen.com)
根据界壳论的基本观点,系统(S)分为周界(A)和系里(B)两部分,即:
![]()
用泛系理论的语言来描述为:
![]()
式中:A为广义软件;B为广义硬件。
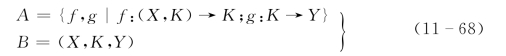
式中:X为系统的输入集;K为系统的状态集;Y为系统的输出集;f为系统内部状态与输入之间的表里、因果关系;g为系统内部状态的外部表现。
式(11-67)、式(11-68)即为界壳的泛系观控模型。
在界壳论中,系里B可用系统输入集X、系统状态集K及系统输出集Y来表征,即B=(X,K,Y)。由界壳论的基本观点,界壳总依附于系统的主体系里,系里不存在了,界壳也随之消失,为界壳的“依附性”特征。同时,界壳的外形、结构,界门的排列、结构和功能等都受制于系里,界壳确定于系里,为界壳的“非任意性”特征。关系f:(X,K)→K体现出的是系里的功能,而关系g:K→Y表现出的是系里的一种观测效果,其功能相当于系里的一个观测器。因此系统周界A一方面能反映出系里B的功能与作用,另一方面也能观测系里B,通过对系里B的观测给控制主体必要的反馈信息,控制主体就能依据该反馈信息做出反应并采取必要的调控手段,对系统的输入、输出进行一定的控制,甚至改变系统的结构、功能,以促进系统的稳定协调发展,从而完成观控过程。因此在一定程度上,界壳可以对系里进行观测与控制,这也符合界壳的“对输入、输出的约束性”特征。在不影响分析结果的前提下,为便于讨论,假设界壳只有一个输入界门和输出界门,则界壳的泛系观控模型如图11-6所示。
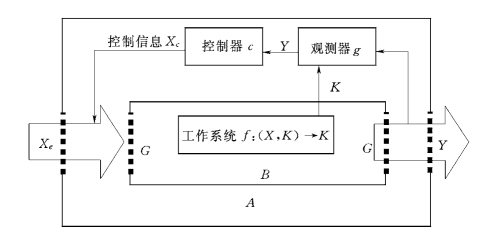
图11-6 界壳的泛系观控模型
图11-6中A为系统周界即界壳,B为系里,G为环境与系统进行交换的通道—界门,f是(X,K)→K的映射关系,它表现为工作系统的功能,这里输入X=Xe∪Xc,其中Xe为环境输入,而Xc为控制主体c依据观测器g所反馈的信息进行的调控措施,观察器g:K→Y所表现出来的是系里状态K的一种观测效果,控制主体c依据观测器g的观测效果采取调控措施,实现对系统的控制。
水资源系统中,界壳包括自然界壳与人为界壳两部分,一个系统当有环境输入Xe时,自然界壳首先参与对系里的观控,得到一个输出Ye,对Ye及期望输出Y进行比较,如果Ye不满足要求,则人为界壳参与作用,通过g、c采取有效的调控措施,对系统实施有效控制,直至系统满足要求。因此人为界壳的作用滞后于自然界壳,比如流域水资源系统,当水资源系统不能满足人类生产、生活及生态需求时,就必须采取有效的调控手段,使水资源系统、社会经济系统及生态环境系统协调发展。当然,随着现代技术的发展,人为界壳的作用也可以达到与自然界壳同步甚至早于自然界壳,比如干旱预报、洪水预报、地震预报等。
11.4.2.5 JC法
JC法从一次二阶矩法、改进的一次二阶矩法发展而来,其不仅可以对非线性的状态方程求解,而且对状态方程中变量的分布不加限定,在风险计算时,达到同等计算精度,计算效率高于蒙特卡洛法,因而越来越受到重视。
JC法用于风险计算的基本计算步骤:


11.4.2.6 模糊风险分析法
水资源系统中许多概念的外延存在着不确定性,对立概念之间的划分具有中间过渡阶段,这些都是典型而客观存在的模糊现象。由于水资源系统的这种客观模糊性,可以应用模糊集理论来研究计算水资源系统的风险,即模糊风险分析法。
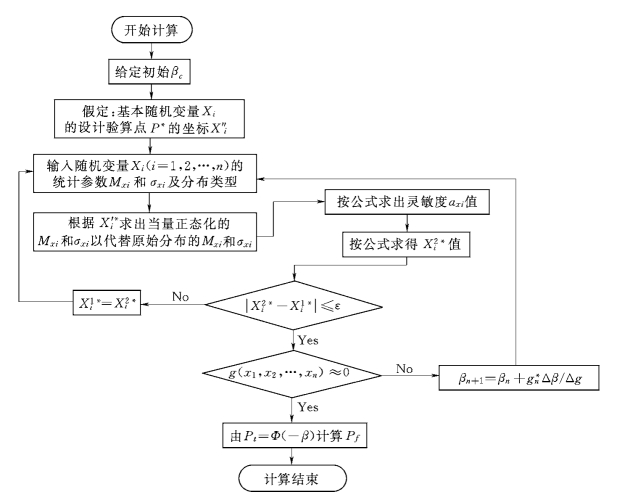
图11-7 JC法流程图

11.4.2.7 灰色风险分析法
在资源系统中,人们可能只把握系统的部分信息或信息所呈现的大致范围,而不知其全部信息或确切信息量,这种部分已知、部分未知的信息称为灰色信息。灰数是描述只知道大概范围,而不知道其确切值的数,记为:

11.4.2.8 其他方法
一些新的风险计算方法,如灰色—随机风险率分析计算方法、极大熵风险分析方法从新的思路出发,丰富了风险分析方法,但由于其理论体系尚不完善,尚需进一步研究,这里仅介绍其基本思想。
1.灰色—随机风险率方法
系统的不确定性,既源于其客观内在的随机不确定性,也源于模型的不确定性、参数的不确定性和获取信息的不足和不精确性,后者归为主观不确定性范畴。对于系统内在固有的随机不确定性的模拟,一般用统计学上的概率,即风险率来表征;而主观不确定性的表征可用概率方法、模糊集理论及灰色不确定性理论。灰色风险率方法则是在随机风险率方法的基础上,强调对风险率的灰色不确定性的描述与量化。
2.最大熵风险分析方法
熵是不确定性或所含信息量的度量,因而可以用熵来计算与不确定性紧密相关的风险问题。
最大熵原理(principle of maximum entropy)是指对于不适定问题,在其所有可行解中,满足一定约束条件时,应选择其熵最大的一个。熵最大意味着此时的解包含的主观成分(人为添加信息)最少,因而是最客观、偏差最小的。“不适定问题”是指求解问题时由于数据不完全或有噪声,或两者兼有,在给定的假设和条件下,不足以推求该问题的确定解。
如前所述,风险分析的基本依据是风险变量的概率特性。在水资源系统风险分析中,许多风险因子的随机特性都无先验样本,而只能获得它的一些数字特征,如均值μ,然而均值μ的概率分布有无穷多个,要从中选择一个分布作为真分布,其优选标准可用最大熵准则。利用最大熵原理确定风险因子的概率分布,实质是将问题转化为信息处理和寻优问题。在用最大熵得到风险变量的概率特性后,应用统计方法就可计算得到风险率值。
由于熵具有对不确定性高层次刻画的特点,因而最大熵风险分析方法具有广阔的应用前景。
