11.5.2 多目标风险决策
多目标风险决策是在风险分析的基础上，把风险指标（风险率或风险损失或两者的组合）同其他指标（效益指标等）放在一起综合考虑，优选出一种最满意方案，使各目标取得最佳权衡。因此，多目标风险决策可采用多目标决策方法。
11.5.2.1 化为单目标求解
在多目标优化问题中，要求所有目标同时达到各自的最优解是很难的，通常是把多目标优化问题化为单目标来求解，多目标化为单目标有许多成熟的方法，如选主目标法、权系数法等。
选主目标法是根据具体情况，从多个目标中选取1个主要目标，其余目标作为约束条件处理，并使之满足一定的要求。
权系数法是对m个目标fi（x）分别给以权系数λi（i=1，2，…，m）（权系数是标准权系数，满足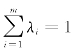
），然后作新的目标函数，该函数变称效用函数，效用函数具有相加、相乘、加乘混合等形式。
相加形式：
为了消除各项目标值之间由于采用的单位不同和数值大小悬殊对方案选择的影响，一种方法是在新目标函数中采用相对值进行计算：
式中：fip（x）为选用的基准方案p的或事先定出的各目标值。
另一种方法是对每个方案的各项目标分别采用百分制或百分经或五分制等进行评分，并乘以各项目标重要性定出的权系数，再把每项目标的得分相加，求得总分数或总平均分数：
或
式中：Fi为每项目标得分数；F∑和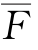
为各项目标总分数和总平均分数。对于难以定量的目标，采用这种评分办法较好。但对于某方案中某项目标完全违背规定要求，得“0”分，则该方案不能采用。
相乘形式：
当得分差距和重要程度差异都很小时，采用相加法和相乘法均为合适。
加乘混合法：
当得分差距和重要程度差异都很大时，必须采用加乘混合法。
平方和加权法形式：要求
。
平方和加权法属于目标规划法，即事先规定一些指标值，再另高目标，看它与这些规定的指标接近的程度。
最小二乘形式：要求
。
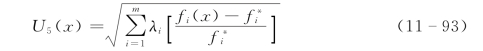
11.5.2.2 序列优化法
序列优化法是对m个目标按其重要性顺序排队，然后从最重要的目标开始，逐个寻优。若已安排好的目标顺序为f1（x），f2（x），…，fm（x），首先对最重要的第1个目标f1（x）求最优，得出最优解f1（x0），并求其他各目标的解，得解集合R0，再在R0内求次重要的第2个目标的最优解，同样也求出其他各目标的解，得解集合R1。这样一直到求出第m个目标的最优解。
从工程问题上，求后一目标最优时，允许已优化的前一目标有一定变化范围作为约束条件，而不必达到严格最优，这样就成为求一系列有变化范围的极值问题：
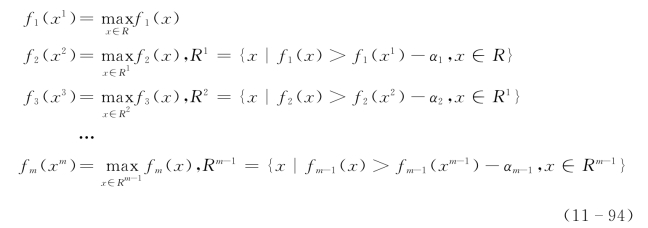
式中：α1，α2，…，αm-1为预先给定的变化范围值。
11.5.2.3 目标规划法
目标规划法按各自指标值fi（x）离决策者所希望达到的各指标值（即最佳水平）
的绝对离差之和最小化进行寻优。其数学表达式为：
式中：di为第i个目标的离差变量。
当考虑各目标优先顺序时，可加入权系数λi，这时目标函数为：
对于一些存在比较明确的指标值作为要求达到的目标的问题和要求考虑各目标优先性顺序的问题，用目标规划法求解较方便。它同序列优化法的思路相同，按重要性顺序逐个寻优。当最重要的第1个目标优化后，进行次重要的第2个目标优化，这时把第1个目标优化后的解固定起来作为1个新的约束条件。同样，当第2个目标优化后，把它的解及连同第1个目标的解一起固定起来作为第3个目标优化时新的约束条件。这样依次类推，直到求得全部目标的解为止。
11.5.2.4 多目标动态规划法
设多目标决策问题：
约束于：
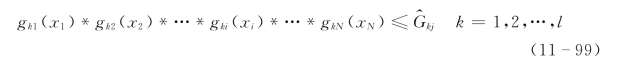
其中
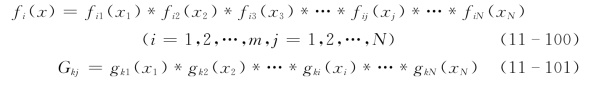
式中：*为运算符，依问题的性质取加号或乘号；x1，x2，…，xN为问题的决策变量组；Gkj为结构状态向量。
多目标动态规划是把其中1个目标作为基本目标，将其余非基本目标处理为状态变量化为单目标动态规划进行递推计算，在递推的最终阶段，不再比较各目标状态下的基本目标值，而将各可行目标状态值连同相应的优化基本目标值一并取出，即为所求非劣解集。
选择多目标中某一目标为基本目标，其他非基本目标处理为状态变量，建立相应模型。如把第1个目标作为单一的优化目标，其余第2～m个目标作为被约束的目标，则可把问题改写为：
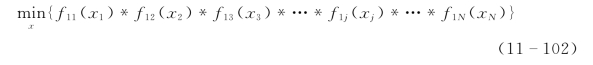
约束于：
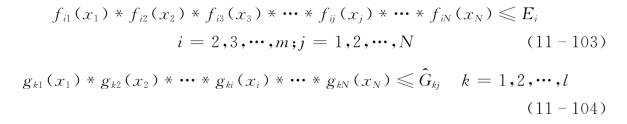
式中：Ei为目标i的最大可接受水平。
递推公式：
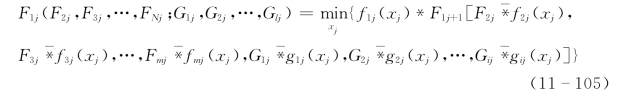
约束于：
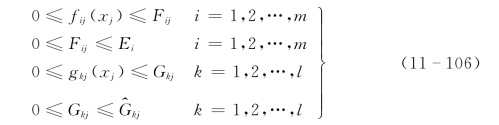
式中：
为与运算符*对应的性质相反的运算符。F1j（·）为主目标函数；Fij为从属于第i个目标函数的状态变量（i=2，3，…，m）。
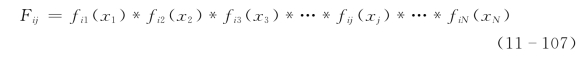
11.5.2.5 多目标模糊优选决策
多目标模糊优选决策依据于优化的模糊性。设有由m个目标，n个待选方案组成的多目标决策问题，每个目标分别有m1，m2，…，mm个评价指标，则对l目标，n个待选方案的评价因素ml个特征值可用下面矩阵表示：
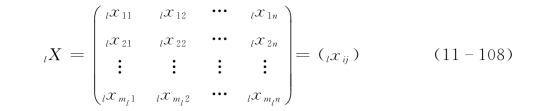
式中：l=1，2，…，m；i=1，2，…，ml；j=1，2，…，n。
11.5.2.6 多目标灰色关联投影决策方法
