5.2.4 水库（群）短期发电优化调度模型
短期调度一般是指以1日或数日为调度期，以15min、30min或60min为时段的一类水库调度问题。其任务是确定各水电站在未来一个调度期逐时段的运行状态或电网负荷在各电站间的分配。短期调度周期较短，是在更接近水库水电站实际运行状况下制订发电计划。它能综合考虑当时水电系统的运行状态（各水库水位、入库流量、机组状况等）和电网的实际状况，来制定水库运行方案，并下达到各水电站进行实施。
水库（群）短期发电优化调度的模型主要有：调度期内发电量最大模型、蓄能最大模型、耗水量最小模型、均匀用水量最小模型及调峰电量最大模型等。
5.2.4.1 发电量最大模型
1.优化调度问题描述
已知调度期（一天或几天）内水库初、末水位（或调度期总用水量）及水库预报来水情况下，考虑满足综合利用要求及各种约束条件，寻求水电站的运行方式，使调度期内总发电量最大。
2.目标函数
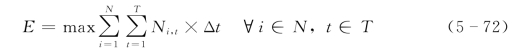
式中：E为调度期内总发电量；Ni，t为i水库t时段平均出力；Δt为时段长；N为水库数目；T为时段数目。
3.约束条件
（1）水库水位（库容）约束同式（5-43）。
（2）水电站出力约束同式（5-44）。
（3）下泄流量约束同式（5-45）。
（4）水量平衡约束同式（5-46）。
（5）若为梯级水库，上下游流量平衡约束为：
式中：τ为水流时滞，在计算中τ通常取平均值。
（6）其他非负约束。
4.适用范围
已知调度期内可用水量，优化电站的各时段出力过程。
发电量最大模型的初水位可取当前实时水位，末水位可从中长期调度结果获得或由决策者根据需要确定。若为梯级水库调度，当调度时段长度较短时需要考虑梯级水电站间的水量传播时间即水流滞时问题。
5.2.4.2 梯级水库蓄能最大模型
见中长期梯级水库群蓄能最大模型。
5.2.4.3 耗水量最小模型
耗水量最小模型是指已知各水库电站初始水位和调度期内总负荷曲线，求水电站（群）在调度期内的最优出力过程。
1.优化问题描述
在保证各时段总发电量要求的前提下，以调度期内各电站出库水量和最小为目标，优化计算各电站的出力过程。此目标是从水调和水能利用角度出发追求的重要指标。
2.目标函数
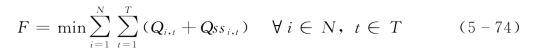
式中：Qi，t为第t时段第i个电站的发电流量；Qssi，t为第t时段第i个电站机组启停对应的流量。
3.约束条件
（1）出力平衡方程：
式中：Ni，t为第i电站第t时段出力；Nf，t为第t时段系统下达负荷。
（2）水库水量平衡方程：
（3）电站出力约束同式（5-44）。
（4）若为梯级电站，考虑水流联系约束。
仅简化考虑水流滞后影响：
式中：Q区i，t为第i电站第t时段区间入流量；τi为第i-1电站至第i电站间水流滞后时间。
（5）电站尾水位—下泄流量关系约束：
式中：
为第t个时段第i个电站的尾水位；fi（·）为第i个电站下泄流量与尾水位关系曲线。
（6）水库水位（库容）约束：
（7）机组开停机限制。根据实际调度要求尽量减少机组的开停次数，并保证机组的最小开停机历时。
（8）电站机组最优特性约束。机组在运行中避开气蚀严重区和高振动区。
4.适用范围
已知未来的一个调度期各时段的总出力或总电量要求，在电站间合理分配负荷，即用电量优化水量。
建立耗水量最小模型时，目标函数除考虑机组发电流量以外，另外还需考虑机组启停费用因素。机组开机费用主要是指：机组从启动到发电并网这段时间内耗费的水量（主要是指冲击启动机组和调整维持水轮机转速寻找并网时机的时间内耗费的水量）和开机过程中因设备的磨损而增加的维护费用；停机费用与开机费用类似。机组每启停一次就会减少机组的使用寿命10～15h，因此有必要考虑机组启停费用。由于机组启停费用目前没有统一的标准，一般将其等价为机组满带负荷3～5min内消耗的水量，为方便计算，可将等价的水量转化为对应调度时段内的流量。
5.2.4.4 均匀用水量最小模型
1.优化问题描述
以满足水电站群系统应承担的负荷图和目标电站（优于日调节性能的水电站）预估用水量（根据长期调度给定）为前提，同倍比增加或减少目标电站的给定用水量。在给定水电系统应该承担的负荷图及目标电站预估用水量时，使目标电站增加用水比例最小。
2.目标函数
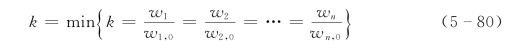
式中：n为目标电站数目；k为用水量比例；wi、wi，0（i=1～n）分别为第i水电站计算用水量与给定用水量。
该目标函数灵活性较好，反映了长期调度的控制，并且体现了各水电站库蓄电能增加或减少的协调关系。
3.约束条件
式中：Ni，l，t，max为i电站l机组t时段的预想出力；k1、k2为反映机组振动与气蚀区域的经验系数（且0<k2<k1<1.0）。
（8）边界约束：
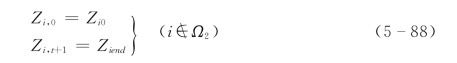
式中：Zi0、Ziend分别为给定的i电站分配期初始水位与终止水位。
5.2.4.5 调峰电量最大模型
水火电联合调度一般以火电费用最小为目标。若能够给定火电系统的综合边际费用曲线，则水电系统可以被分解出来独立进行优化调度。
为了间接考虑火电机组出力不宜变动太大的特性，建立调峰电量最大模型。其含义是：经水电系统削峰后，使整个电力系统的剩余负荷在保证平坦的情况下尽可能的小。
调峰电量最大模型分为2个模块：周期性模型和过渡模型。前者反映了水电站持续运行的理想模式，由于水电站实际运行总是与理想模式有所偏差，需要在实际运行中优化过渡。周期性模型中，在周期运行日控制期内最后一天（若控制期小于一天则进行延长），通过优化可确定控制期末各水电站滞时区出库流量和各水库的末水位。
（3）固定滞时区出库流量：
式中：Q出i，t，cyc为周期性模型优化所得控制期末出库流量。
（4）初始开停机状态、电站开停机次数和持续时间要求。
以上约束中，t=0，1，…，T-1，当t<0时，表示控制期初以前。
直接用模型中的目标函数不利于模型求解。首先是收敛速度较慢，当余荷最大时段出力有所改变时，目标函数才会随着变动；其次是负荷低谷时段容易产生弃水，这不符合实际调度情况；而且，当有2个以上时段的余荷同为最大余荷时，只有这些时段的余荷同时降低，目标函数才会改进，这是很难做到的。因此，在求解时寻求一个替代目标，更容易求解而且能达到模型所期望的效果。