3.6.3　模糊神经网络预测算法

3.6.3　模糊神经网络预测算法

设待预报对象Y有n个样本，即：

经成因分析和历史实际记录资料分析知，每个样本对应着m个预报因子的特征值，对于n个样本，则有预报因子特征值矩阵：

由于各预报因子的物理量不尽相同，量纲不同，需要确定预报因子特征值矩阵的相对隶属度矩阵，即：

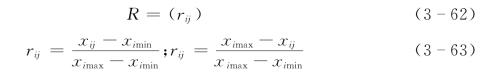
式中：xij为样本j预报因子i对模糊概念的相对隶属度；ximin、ximax分别为对应于参考连续系统上相对隶属度的左极点0和右极点1。当预报因子特征值与预报对象呈正相关时，xij介于ximin与ximax之间的相对隶属度呈负相关，相应地，预报对象预报因子的特征值的相对隶属度向量为：

其中：

式（3-63）、式（3-64）构成了模型输入、输出的样本集。模型的输入节点数为m（预报因子数），输出节点数为l（预报对象数）。用i表示输入层节点，p表示输出层节点。在输入层，节点i将信息直接传递给隐含层节点，故第j个样本在输入层节点i的输出uij与网络输入rij相等。

隐层节点用h表述，隐层节点数等于标准模式数C，其大小根据样本容量的多少确定。标准模式向量为S=（s1，s2，…，sc），可以在0～1之间划分。

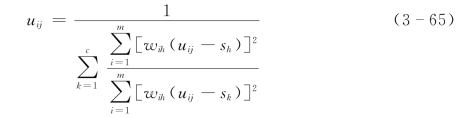
网络隐层节点的激励函数为模糊模式识别模型。

式中：wih为输入层节点i的输入对隐层节点h的输入权重；j为样本号。

网络输出节点p的激励函数采用模糊优选模型为：

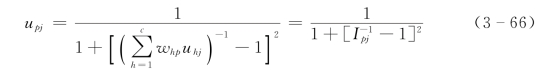
式中：whp为隐层节点h与输出层节点p的连接权重；j为样本号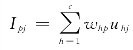；。