3.7.3　改进的最小二乘支持向量机

3.7.3　改进的最小二乘支持向量机

将式（3-88）的优化泛函改进为如下形式：

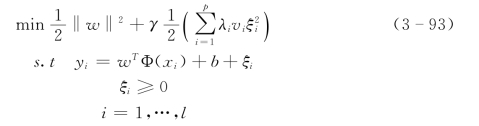
式中：vi=yi/ymax为峰值识别系数；λi为vi的放大系数。

同样，求解式（3-94）的优化问题，引入Lagrange函数：

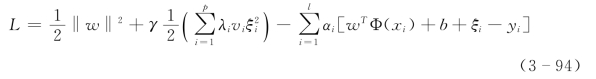
最优的αi和b根据KKT（Karush-Kuhn-Tucker）条件得到：

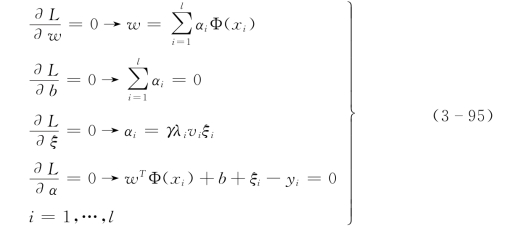
由式（3-96），优化问题转化为求解如下的线性方程：

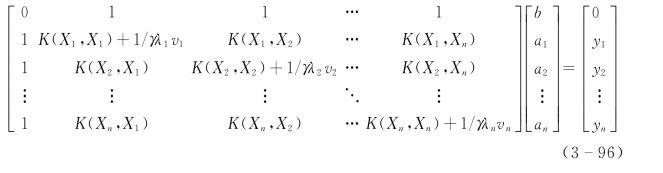
得到非线性回归函数的解为：

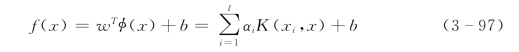
称为峰值识别最小二乘支持向量机模型（λivi-SVM模型）。

SVM是一种有坚实理论基础的新颖的小样本学习方法。它基本上不涉及概率测度及大数定律等，因此不同于现有的统计方法。从本质上看，它避开了从归纳到演绎的传统过程，实现了高效的从训练样本到预报样本的“转导推理”，大大简化了通常的分类和回归等问题。

由于有较为严格的统计学习理论作保证，应用SVM方法建立的模型具有较好的推广能力。SVM方法可以给出所建模型推广能力的严格的界，这是目前其他任何学习方法所不具备的。建立任何一个数据模型，人为的干预越少越客观。与其他方法相比，建立SVM模型所需要的先验干预较少。

但核函数的选定及有关参数的优化、模型训练和测试速度等问题仍是目前尚未很好解决的问题。SVM通过核函数实现到高维空间的非线性变换，所以适合于解决本质上非线性的分类、回归和密度函数估计等问题。