3.3.5 马尔科夫法(随机型)
20世纪初,俄国数学家马尔科夫(A.A.Markov)在研究中发现自然界中有一类事物的变化过程仅与事物的近期状态有关,而与事物的过去状态无关。具有这种特性的随机过程称为马尔科夫过程。
马尔科夫预测法是现代预测方法中的一种,它具有较高的科学性、准确性和适应性,在现代预测方法中占有重要地位。在国外,它不仅广泛应用于自然科学领域,还应用于经济领域。在我国它主要应用于水文、气象、地震等自然科学技术领域的预测。
马尔科夫预测法的基本原理有两个主要内容,即方法的基本思想和体现基本思想的预测模型。关于这种方法的基本思想,马尔科夫通过实践认为:世界上无论是社会领域还是自然领域,有一类事物的变化过程只与事物的近期状态有关,与事物的过去状态无关。事物的这种性质称为无后效性。例如事物S,从初始状态S0起,其变动过程的状态可记为S1,S2,…,Sn-2,Sn-1,Sn。事物经过n次变动后,第n次变动的结果,仅仅与近期(n-1)次的结果有关,与(n-1)次以前的各次变动无关;又如,事物的第(n-1)次的结果,仅仅与近期(n-2)次的结果有关,与(n-2)次以前的各次变动无关;……;亦即,某一次变动只能影响到它的下一期,再往后就没有影响了。这就叫做状态转移的无后效性。如果n个连续变动的事物,在变动的过程中,其中任一次变动的结果都具有无后效性,那么,这n个连续变动事物的集合,便叫做马尔科夫链,这类事物演变的过程称为马尔科夫过程。
遵从马尔科夫基本思想变动的事物,应具有两个主要特点:第一,表明事物在过程中的变动是随机的,因此马尔科夫过程是一个随机变动过程。第二,事物每一次变动的结果都具有状态转移的无后效性。
对马尔科夫链进行分析可知,变动过程中的事物由一种状态随机地变成另一种状态,必然要经过一个中间变化过程。这个中间过程的表现形式称为转移状态。根据无后效性原则,知道事物的状态应与事物的转移状态相关,即是事物的前状态、后状态、转移状态三者相关。为此,设事物的前状态为Sn-1,后状态为Sn,转移状态为P,则三者的关系为:
![]()
根据以上的关系式,可以得到两个结果:①如果转移状态为已知,可以根据上期信息资料,预测事物本期变动的结果;②根据本期和转移状态,可以预测下期情况或下几期的情况。
为了论述和计算的方便需要,引入下列有关概念。
1.转移矩阵
设系统的状态转移过程为一齐次马尔科夫链,状态空间为S=(0,1,2,…,n),状态转移概率为Pij,则称矩阵
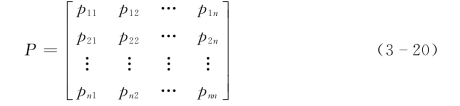
为该系统的状态转移概率矩阵,简称转移矩阵。
2.概率向量
对于任意的行向量(或列向量),如果其每个元素都是非负且总和等于1,则称该向量为概率向量。
3.概率矩阵
由概率向量作为行向量所构成的方阵称为概率矩阵。
设变量所处的状态数有n个,记为S1,S2,…,Sn。
记变量从状态Si经过r步转移到状态Sj的转移概率为![]() ,那么称矩阵
,那么称矩阵
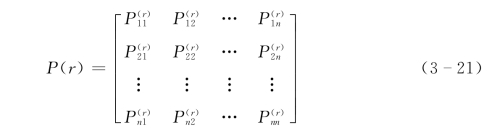
为r步转移概率矩阵。当r=1时,P(1)简记为P。显然有:
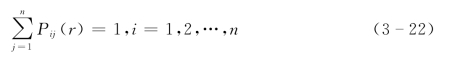
由概率论和线性代数知识易证:
![]()
4.算例(https://www.daowen.com)
采用表3-7中的数据,预测2000年、2001年的需水量。
(1)划分状态区间。
将需水量按由低到高的顺序划分为6个状态空间,见表3-10。
表3-10 状态空间的划分

(2)计算状态转移概率。
1)状态转移矩阵,如下表所示。
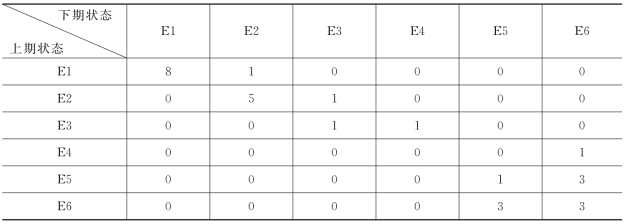
2)计算状态转移概率,如下表所示。
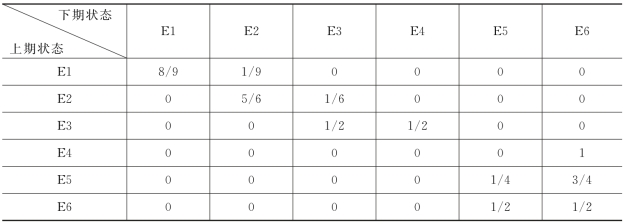
得状态转移概率P为:

(3)计算初始状态向量。
以1999年作为基期,由资料得知该时段初始状态向量为:
p(0)=(0 0 0 0 0 1)
(4)预测2000年的需水量。
计算如下:

由p(1)=(0 0 0 0 1/2 1/2)分析可得2000年的需水量可能发生在状态E5或E6,即落在(580~640)或(640~∞),其落在这两个状态空间的概率相同。
(5)预测2001年的需水量。
计算如下:

分析知2001年需水量发生在状态E6的概率为最大。
