8.3.5 临界调控专家系统的推理机
控制专家系统中推理机的任务是以知识库中的已有知识为基础,模拟专家的思维过程,为调控提供理论依据。这里专家思维主要有两层次含义,一是定量计算,即系统有序度的计算;另外是定性推理,即系统演化方向的推理。图8-7为多维临界调控专家系统推理机的组成。
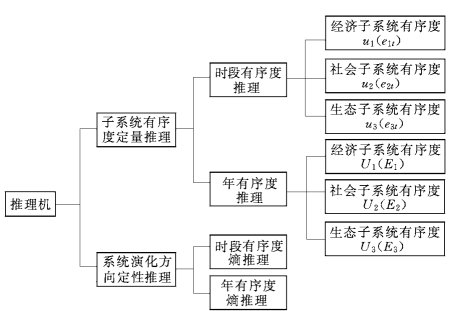
图8-7 多维临界调控专家系统推理机组成
8.3.5.1 有序度(协调度)
水资源系统是耗散结构,系统的相变结果不一定都走向新的有序,也可能走向无序,因此为了把握系统协调的程度,以促使系统向更加有序的方向转化,有必要在临界调控之前,首先计算在某种利用方案下序参量的协同作用。为此,引入有序度(协调度)这一概念来衡量协同作用。
考虑子系统Sj,设其发展过程中的序参量变量为ej=(ej1,ej2,…,ejn),其中n≥1。eji的取值应在临界阈值区间,如:βi≤eji≤αi,i∈[1,n]。假定ej1,ej2,…,ejm(1≤m≤p)在阈值区间的取值越大,子系统的有序程度越高,其取值越小,子系统的有序程度越低,如经济子系统中的工农业供水量;假定ejm+1,…,ejp(m≤p≤n)在临界阈值区间的取值越大,子系统的有序程度越低,其取值越小,子系统的有序程度越高,如生态子系统中的污染物含量等;假定ejp+1,…,ejn在临界阈值区间越接近某一值c,子系统有序程度越高,如社会子系统中凌期控制断面流量。这样,针对黄河流域水资源系统给出如下有序度的计算。
定义子系统Sj序参量分量eji的有序度为:
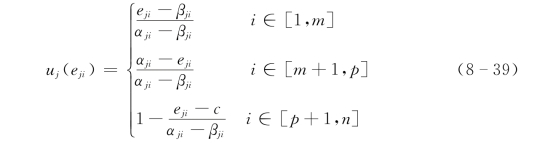
式中:uj(eji)为序参量分量eji的有序度。
由上式可知,若序参量eji的有序度值uj(eji)∈[0,1],则序参量在临界阈值区间,且其值越大,eji对子系统Sj有序的“贡献”越大;相反,若eji∉[0,1],说明eji不在合理阈值区间,需进行调节。从总体上看,序参量变量eji对子系统Sj有序程度的“总贡献”可通过uj(eji)的集成来实现,如式(8-40)所示:
![]()
uj(ej)称为子系统Sj序参量ej的有序度,且uj(ej)∈[0,1]。uj(ej)越大,ej对整个系统有序的“贡献”越大,系统有序的程度就越高;反之则越低。λi为序参量分量eji的权系数,它的确定既应考虑到系统的现实实际运行状况,又应能够反映系统在一定时期内的发展目标,其含义是序参量分量eji在保持子系统有序运行中所起的作用或所处的地位。
对控制对象模型得出的黄河流域水资源开发利用方案,通过专家系统推理机就可计算该方案下各子系统的有序度,作为控制者调控的依据。利用专家系统推理机即可得出每个计算时段(月、旬)经济、社会和生态子系统的有序度,用于对每个时段的水资源利用情况进行调控,也可计算出年有序度,实现对年方案的调控。
8.3.5.2 黄河流域水资源子系统时段有序度的推理
1.经济子系统有序度u1(e1t)
从时段角度讲,经济子系统的序参量包括该时段的供水量e11t和时段出力e12t,t代表时段。这两个序参量都属于越大越优型。
(1)生活、工农业供水量e11t的有序度。序参量e11t由10个分量组成,e11t=(e11t1,e11t2,e11t3,…,e11t10),e11ti代表第t时段给第i个省区的供水量,i∈[1,10],依次为青海、四川、甘肃、宁夏、内蒙、山西、陕西、河南、河北、天津和山东。则供水量分量e11ti的有序度为:(https://www.daowen.com)



8.3.5.3 黄河流域水资源子系统年有序度的推理
1.经济子系统有序度U1(E1)
对于某一调度年份,经济子系统的序参量与时段序参量类似,包括年度总供水量E11和年度总发电量E12。这两个序参量都属于越大越优型。




8.3.5.4 黄河流域水资源系统演化方向的定性推理
由于特定时段内水资源量的有限性,子系统之间存在着相互竞争,子系统的有序度并不能代表整个黄河流域水资源系统的有序度。经济、社会、生态子系统的有序度不可能同时增加,某一个子系统有序度的提高,可能会导致其他子系统有序度的降低,但是整个系统的有序度如何变化却无从确定,这也是水资源系统临界调控需要解决的问题。
耗散结构的熵理论为我们解决这个问题提供了依据,虽然熵并不能对系统演化进行定量计算,而且也不易于用显式函数表示出来,但利用熵与有序度之间的关系,可以对系统演化方向进行定性分析,即熵减少,有序性增强,熵增大,有序性减弱。
根据信息熵的定义,利用子系统有序度可建立判别水资源系统演化方向的有序度熵(协调度熵)函数。式(8-57)为年有序度熵函数:



