3.8.3 小波分析在需水时间序列组成分析中的应用
小波分析(WaveletAnalysis)是近年发展起来的一门新的数学分支,由于小波函数具有许多优良特性,现已成为众多学科研究的热点,并已广泛应用于信号处理、图像处理、语音合成和处理、模式识别和地震勘探等非线性科学领域。水资源需求是一种社会现象,需水时间序列是一个统计样本,是一种离散信号。如何把合成序列中的各种成分划分出来,并采用适当的数学模型去描述这些成分,是需水序列机制的重要研究内容。小波分析通过将需水序列信号分解成一族小波函数(由同一母小波或基小波演化而来,称小波变换),借助于小波函数特征,便可以同时从时频域上分析需水序列信号的时序特征,且其采样步长是可调的。对于需水序列信号中的高频特征,采样步长较小;而对于需水序列信号中的低频特征,采样步长较大,因而小波分析具有局部放大作用。同时小波分析中选用同一个基函数,在对其进行伸缩和平移中,保持自相似结构。这对于分析需水时间序列具有很大的优越性。
下面以需(用)水时间序列为例,利用小波分析时频局化性质分析用水的变化特征,了解在不同时间尺度上的详细结构及变化规律,并将用水时间序列的趋势项、细节项的不同频率成分分离,以便预测未来需水的长期变化过程。
以1970~1999年的黄河流域需水序列数据作为测试样本,利用MATLAB的小波工具箱的‘db6’函数,对资料进行三层分解得到细节序列D1、D2、D3和近似序列A3。具体步骤如下。
(1)原始数据的分解。利用MATLAB小波工具箱中的‘db6’函数,对数据作了三层分解,其程序如下:
x=[340.63,342.74,347,350.5,352.3,356.3,360.5,374.4,385.05,412.93,415.2,422,428.5,437.5,444.73,461.89,479.31,547.31,697.54,610.79,649.52,656.7,650.1,627.16,644.01,626.08,591.54,647.35,671.87];
ls=length(x);
cA3=appcoef(C,L,′db6′,3);
cD3=detcoef(C,L,3);
cD2=detcoef(C,L,2);
cD1=detcoef(C,L,1);
A3=wrcoef(′a′,C,L,′db6′,1);
D1=wrcoef(′d′,C,L,′db6′,1);
D2=wrcoef(′d′,C,L,′db6′,2);
D3=wrcoef(′d′,C,L,′db6′,3);
subplot(2,2,1);plot(A3);title(′近似部分A3′)
gridon
subplot(2,2,2);plot(D1);title(′细节部分D1′)
gridon
subplot(2,2,3);plot(D2);title(′细节部分D2′)
gridon(https://www.daowen.com)
subplot(2,2,4);plot(D3);title(′细节部分D3′)
gridon
可以得到细节序列D1、D2、D3和近似序列A3,如图3-10所示。
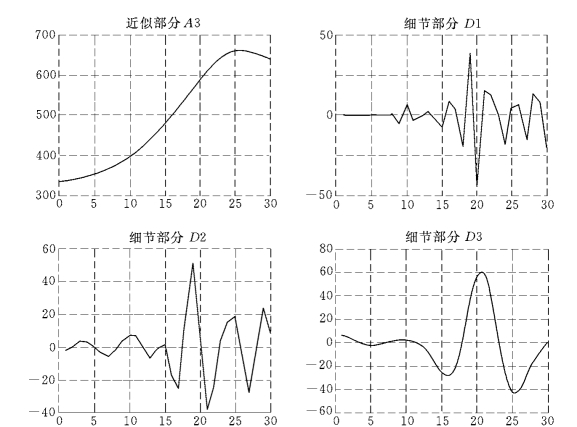
图3-10 三次分解产生的分解序列图
(2)分解后数据的获取。从分解后的图像中逐个摘取数据,把图表还原为数据序列。
(3)各序列的预测。利用神经网络工具ANN,对上述的4个数据序列分别预测,即得到4个预测序列(表3-25)。
(4)小波的重构。根据小波分析产生的子序列的不同特点,分别选取不同数量的过去时间点数进行预测。第j层分解采用的过去时间点的数目为rj,令
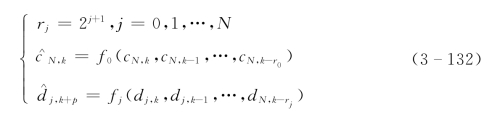
其中:f0,f1,…,fN分别为预测函数。函数fj建模的数据个数为rj个。图3-11中实线表示小波分解生成的子序列,虚线表示神经网络预报的结果。将所有子序列的预测结果线性相加,就可以得到原序列的预测值:
![]()
其结果见表3-18。
表3-18 预测结果表
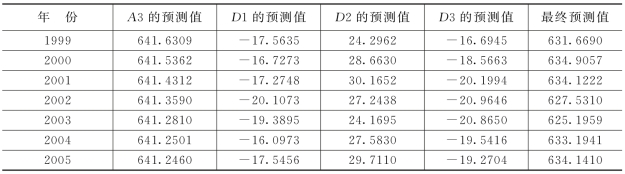
实际值与预测值的比较见表3-19。
表3-19 实际值与预测值的比较

我们以1970~1999年的需水量数据作为测试样本,测试结果见表3-18。采用神经网络模型对周期成分和趋势成分进行预测,预测步长为1年,得到1999~2005年需水量的趋势和周期成分,然后与纯随机成分重构得到年径流序列,各成分的预测过程线和实测过程线如图3-10、图3-11所示,预测效果见表3-19。由该表和图3-11可以看出,该小波神经网络的预测可达到精度要求。预测的相对误差最大为5.9%,达到了很高的精度。鉴于此,我们应用上述小波和神经网络相结合的预测模型对1999~2005年的需水量进行预测,结果如图3-11所示。
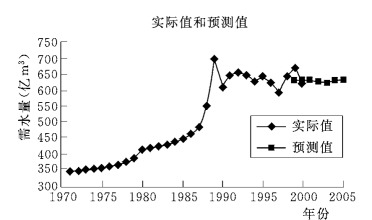
图3-11 预测结果分析图
