5.2.5 水库(群)短期发电优化调度模型的求解方法
水库(群)中长期发电优化调度模型的求解方法,如DP、DPSA、POA、GA、大系统分解协调法、蚂蚁算法等优化算法也可用于求解水库(群)短期发电优化调度模型,不同的是调度期时段的划分以及需要考虑梯级水库间的水流滞时等问题。
5.2.5.1 等微增率法
等微增率法仅适用于求解短期发电优化调度的耗水量最小模型,本节以梯级水库群为例说明其模型方法。
等微增率原则以两台机组之间的负荷分配为例,两机组的流量特性曲线如图5-8所示,从图中可以看出,当分配给机组Ⅰ的负荷为N1,机组Ⅱ的负荷为N2时,两台机组在各自流量特性曲线上的工作点分别是a点和b点。此时若增加机组Ⅰ的负荷,机组Ⅱ势必减少相应地负荷以保证出力的平衡,即dN1=-dN2,这样,机组Ⅰ的工作流量将增加dQ1,机组Ⅱ的工作流量将减小|dQ2|(即dQ2为负值)。
在机组流量特性曲线上,随着出力的增加,曲线的斜率逐渐增大,因此有|dQ1|<|dQ2|,因而电站的总工作流量变化值dQ=dQ1+dQ2<0,这就意味着,增加机组Ⅰ的负荷,减小机组Ⅱ的负荷可使电站总工作流量减少,从而给电站带来经济效益。
在保证出力平衡条件下,继续增加机组Ⅰ的负荷,减小机组Ⅱ的负荷,在某两点上,两机组流量特性曲线的斜率相等,即:
![]()
此时,dQ=dQ1+dQ2=0电站达到最佳运行状态。所以,在给定负荷下,水电站耗水最小的条件是两台机组的流量微增率相等。以上的分析方法可以推广到n台机组的情况。
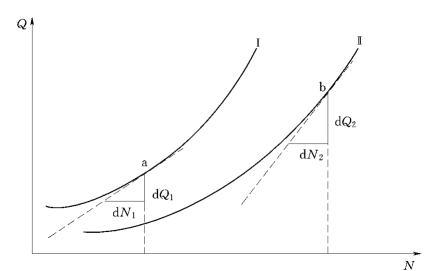
图5-8 两机组的流量特性曲线
如果将整个梯级水电站视为一个水电站对待,将各电站看作一个个“机组”,在给定负荷条件下,梯级的耗水最小模型同样可以用等微增率原则来求解,具体求解步骤如下。
(1)读取第t时段(t=1,2,…,T)的梯级总负荷Nf,t,按照各电站的装机容量比例对负荷进行初始分配,由各电站应承担系统负荷,即出力Ni,t分别计算相应的耗水量Q出i,t并计算梯级的总耗水量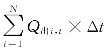 。
。
(2)计算各水电站的流量微增率:给各电站的出力增加一单位增量ΔNi,并计算流量的增量ΔQi。
(3)对流量微增率ΔQi进行排序,找出最大者和最小者并标记对应的水电站,若|maxΔQi-minΔQi|<ε计算结束,否则转下一步。
(4)将微增率最大的水电站的出力减少一定比例,并将减小的出力增加到微增率最小的电站上,如果此电站已达当前条件下的约束边界(出力上下限、水位上下限、流量上下限等),则将多余部分增加到微增率次小的电站上,重新计算各电站耗水量及梯级总耗水量。
(5)计算各水电站的流量微增率并排序,若|maxΔQi-minΔQi|<ε,则计算结束,否则转步骤(4)。
5.2.5.2 二倍体遗传算法
二倍体遗传算法(DGA)求解水电站短期优化调度问题,是借助于基因显性机制,利用二倍体基因结构具有内在的保护群体基因多样性的能力,来提高算法的全局寻优能力。算法中,出力限制条件在调度方案的编码中自动满足,而其他约束条件如负荷平衡、水量平衡等则在计算个体适应值时予以考虑。应用遗传算法求解水电站短期优化调度问题的关键是:确定调度方案(个体)的编码表示方式;个体的适应值计算;遗传算子的实现。下面以梯级水电站群为例,说明其求解方法。
1.个体的二倍体编码表示
选择电站各时段的出力作为编码变量,将各编码变量的取值范围等间隔离散,用一个二进制码表示,其长度L取决于计算精度的要求。那么,所有变量的编码按顺序连接起来组成一条长度为L的二进制码链,如图5-9(a)所示。按照确定的编码关系,任意一条长度为L的二进制码链都对应一个调度方案(可行或不可行),显然,在编码中已满足了电站出力约束条件。个体的二倍体编码表示就是以两条等长度的二进制码组成一对表示个体,如图5-9(b)所示。这种表示方式更接近于自然界中生物组织的基因染色体结构。
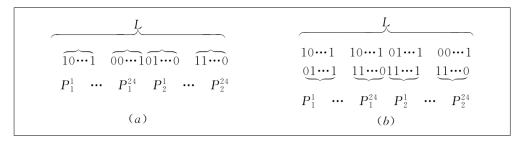
图5-9 个体表示方式
(a)调度方案编码;(b)个体的二倍体表示方式
利用基因显性算子,个体的两条基因链可以映射为一条与基因链等长度的二进制码链,称为个体的功能码。按照图5-9(a)确定的编码关系,个体功能码解码为原问题的一个调度方案。基因显性算子按下面的布尔运算式实现:
![]()
式中:ch1(k)、ch2(k)分别为个体的两条基因链;ds为群体的基因选择参考链;cs为个体的功能码链;k为码链的第k位。
初始群体的基因选择参考链是随机产生的,在进化中,可选择上一代群体中最好个体的功能码链作为本代群体的基因选择参考链。
2.个体的适应值计算
以具有2个水库的梯级水库群日优化调度为例,计算个体适应值时首先按照上述方法,进行二倍体编码,其中每个个体基因链可以解码对应一个调度方案,即每个时段的各电站的出力。将调度方案代入目标函数及约束条件逐时段进行以下操作:根据电站水头特性和机组流量特性计算本时段电站的水头和发电流量;由水量平衡方程计算本时段末水库存水量及本时段的弃水量;由梯级电量平衡约束计算本时段出力偏差;由水电站水量约束条件计算本时段对流量、水位约束条件的违反量。最后将计算结果代入目标函数计算调度方案相应的目标函数值J。从上述计算过程可以看出,由于采用水量平衡方程直接计算水量平衡,因此水库间的水流流达时间自然得到了考虑。个体的适应值是算法中衡量个体相应调度方案优劣的一个度量。对于一个调度方案,若目标函数值大,对约束条件的违反量小,没有弃水或弃水少,则方案好,其相应的个体应该赋予一个大的适应值。因此,可按下式计算个体i的适应值FITi:
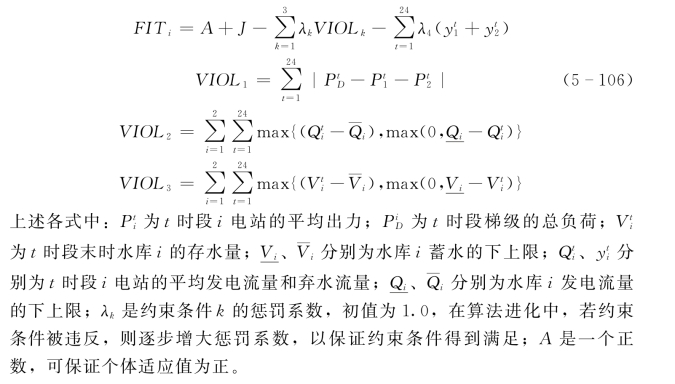 (https://www.daowen.com)
(https://www.daowen.com)
3.遗传算子
在DGA中,选择算子和变异算子的方法与单倍体遗传算法雷同。选择算子以个体适应值占群体总适应值的比例为选择概率,选择个体进入下一代群体。变异算子以小概率确定个体每个基因是否变异,若发生变异,则将基因值取反。杂交算子由以下两个步骤完成。
(1)个体基因链交换,两个个体之间随机交换一条基因链组成两个新个体。
(2)个体基因混合重组,新个体的两条基因链按照一致杂交算子方式进行杂交,以实现基因链之间的信息交换。
4.局部搜索算子
在应用遗传算法时,经常遇到这样的情况:算法进化到一定程度后,最好个体已进入到了最优解附近的一个不大的范围内,但算法进一步将最好个体推向最优解的过程却变得非常缓慢。原因是由于算法进化后期,群体中的个体基因模式接近相同,难以产生更高阶的优良模式。
在遗传算法中,应用局部搜索算子有利于改善这一状况。采用爬山法实现局部搜索。随机产生一个优化变量,将该变量对应的编码段加1和减1,于是形成两个新个体,将质量好的新个体替代原个体。爬山算子不在有利的方向进一步搜索,是为了避免由于爬山算子的作用而引起某一个体的适应值远远高于其他个体的适应值,从而避免在进化初期算法收缩于某一个体所在的局部区域,影响算法对全局的搜索能力。
5.二倍体基因遗传算法步骤
(1)随机产生2M条长度为L的二进制码链,组成初始群体的M个个体;随机产生一条长度为L的二进制码链作为初始群体的基因显性参考链。
(2)对群体迭代地执行下面的步骤,直到满足停止准则。
1)按照式(5-105)计算群体中每个个体的功能码链,解码后代入目标函数约束条件中分别计算个体相应的目标函数值及对各约束条件的违反量,代入式(5-106)计算个体的适应值。
2)将当前群体中适应值最大的个体的特征链作为下一代群体的基因显性参考链。
3)应用选择、杂交和变异算子产生下一代群体;当前群体中的最好个体保留进入下一代群体;应用局部搜索算子对最好个体进行操作,改善算法的局部搜索能力。
(3)将得到的最好的个体指定为算法的执行结果。算法的停止准则可采用:算法已进化了预先指定的代数或者算法经历了若干代进化,而最好个体的适应值已没有改善。
求解梯级水电站短期优化调度问题的二倍体遗传算法的主要优点有:计算中直接采用机组流量特性,而不采用近似的电站综合流量特性,提高了计算精度;计算时间短,所需内存少;算法中易于考虑各种限制条件,如负荷平衡、出力限制、流量和水位限制等,并且容易考虑梯级水库间的水利联系和水流滞时的影响。
5.2.5.3 模糊动态规划
模糊信息在水库调度中是普遍存在的,例如入库流量和出库流量。其中入库流量既受环流形势和天气系统、地理位置和地形地貌等自然因素影响,又受人类生产活动、预报人员分析水平、发布预报时的心理等社会因素影响。所以水库入库流量得到的信息是具有模糊性的。即通常所说的“大雨”、“中雨”、“小雨”或入库流量“偏丰”、“偏枯”、“正常”等都是模糊概念,没有明确的外延。出库流量客观上具有模糊性,也是受上述各因素影响产生的,不过,社会因素大些。例如,某综合利用水库以发电为主,在汛期和非汛期的过渡段中(汛期和非汛期是模糊概念),水库下泄流量便受多方面因素影响。此外,还有一些“软约束”,例如库容约束并不是严格的约束条件,而是可以“适当违反的”——这类约束条件本质上也是模糊的。正是由于存在以上这些模糊现象和信息,于是产生了模糊优化调度方法,它以模糊集合论为基础,并与常规调度技术、优化调度技术融为一体,互相取长补短,克服了传统方法处理模糊信息及模糊现象所遇到的困难,以寻求满意的调度方式、调度方案和调度图,指导水库运行。
模糊优化模型具体又分为对称优化模型和非对称优化模型2种,下面介绍采用对称优化模型的方法来求解水库日优化调度模型。.
优化问题的求解,主要是如何处理模糊约束条件。模糊约束主要有2个:
(1)各电站的出力要大致等于对它的负荷要求,通过给定一个偏差系数θ,可以形成负荷“廊道”,其上下限为:
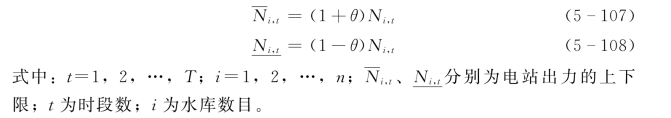
(2)水库库容约束,在传统优化中是作为罚函数来处理的,但是罚系数的选取没有一个统一的标准,选择不当会引起问题无解。因此采用模糊动态规划的方法来求解。
求解梯级水库日发电量最大优化调度模型步骤如下。
(1)确定水库库容约束条件的隶属度函数。
(2)求目标函数的无条件模糊优越集:这里把目标函数作多目标来处理,即把梯级的总发电量看作各级电站目标发电量之和。若各电站发电量单位不同,则存在着目标的不可公度性,因此将各目标分别进行模糊化。于是总发电量的模糊隶属度应为各电站发电量的模糊隶属度之和。
(3)已知各水库的初始库容和水位,根据第一个水库日来水情况和可能的日下泄流量预估该水库日库容和流量的最大最小范围,对此范围进行离散。同理,对其余电站也可得到一系列离散点。
(4)在多阶段模糊决策中,模糊目标是通过最终时刻T的系统状态VT的隶属度函数来评价的。因此,寻找目标最大化,就是要找到最优策略。
采用动态规划逆推计算求解,得到各时段的递推方程。最后,使隶属度取最大值的解即为最优解。
综上所述,应用模糊优化技术求解有约束、多阶段、模糊、非线性的复杂梯级水库优化调度问题,在常规模糊优化的基础上改进了目标函数的无条件模糊优越集,使优化结果得到提高。通过实例仿真的结果表明,模糊动态规划的方法可以被有效地应用于梯级水电系统的短期优化中,其主要优点是可以方便地同时处理模糊及非模糊目标和约束条件,且不用考虑目标函数是否连续可微。
