3.5.4　模型检验

3.5.4　模型检验

GM（1，1）模型有残差检验法、关联度检验法和后验差检验法。残差检验法是指按所建模型计算出累加序列，再按累减生成法还原，还原后将其与原始序列X（0）相比较，求出两序列的差值即为残差，通过计算相对精度以确定模型精度；关联度检验法是按式（3-40）计算；后验差检验法是指按所建模型先分别求出原时间序列和参差序列的均值和方差，再计算两者的方差比及预测误差的小概率。

如果相对精度均满足要求精度，则模型通过检验；如果不满足要求精度，可通过上述残差序列建立残差GM（1，1）模型对原模型进行修正。残差模型GM（1，1）可提高原模型的精度。

1.残差检验

模型绝对误差为：

相对误差为：

2.关联度检验

其中：min{|ε（0）（i）|}=min{|ε（0）（1）|，|ε（0）（2）|，…，|ε（0）（n）|}

max{|ε(0)(i)|}=max{|ε(0)(1)|,|ε(0)(2)|,…,|ε(0)(n)|}

ρ为取定的最大差的百分比，一般可取0.5，即50%。

3.后检验

先求原时间序列的均值和方差：

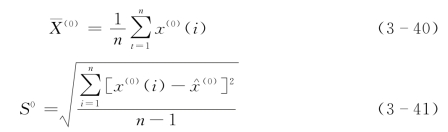
再求残差序列的均值和方差：

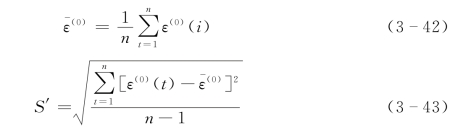
由上面结果可求方差比：

预测误差小概率P为：

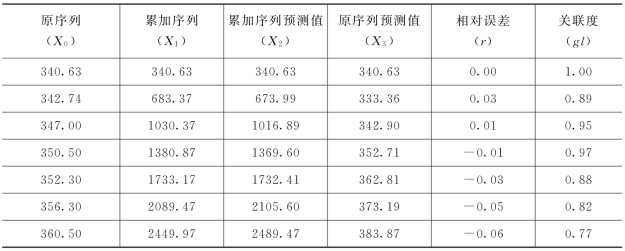
根据以上求得的各参数可划分级数来确定所建模型的精度等级。计算结果见表3-11。

表3-11　GM（1，1）计算结果　单位：亿m3

综上所述，GM（1，1）模型实质上是采用线性化方法建立的一种指数预测模型。因此，当系统呈指数变化时，预测精度最高。