3.3.6　博克斯—詹金斯法（随机型）

博克斯—詹金斯法，简称B-J法或ARMA模型法，是一种针对剧烈震荡的平稳随机时间序列进行短期预测的有效预测方法。该方法假定时间序列的变化与自身过去的历史数据有关，建立自相关的回归模型以及它的变形：移动平均模型，将模型外推做出预测。由于真实的时间序列不一定是平稳的，可能是有线性增加趋势或是周期变化，可以对原始的时间序列进行差分来解决趋势与周期变化问题对建模的干扰。

博克斯—詹金斯法应用到水资源需求预测中的基本思想是：将水资源需求随时间推移而形成的历年用水数据序列视为一个随机序列，即除去个别的因偶然因素引起的观测值，使用水时间序列成为一组依赖于时间t的随机变量。这组随机变量所具有的依存关系或自相关性表征了水资源需求发展的延续性，而这种自相关性一旦被相应的数学模型描述出来，就可以以用水时间序列的过去值及现在值预测其未来的需求值。

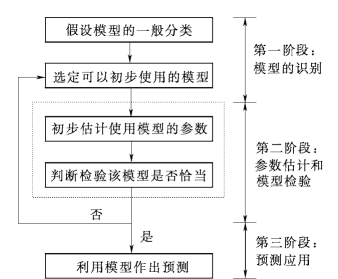
博克斯和詹金斯在说明他们的预测方法时，曾绘制了如图3-2所示的预测流程图。该方法把预测问题划分为3个阶段：①模型的识别，即初选模型；②模型中参数的估计和模型检验；③预测应用。

图3-2　博克斯—詹金斯法预测流程图

第一阶段：利用自相关分析和偏自相关分析等方法，选定一个特定的预测模型以拟合所分析的用水时间序列数据。模型的识别是博克斯—詹金斯法预测中至关重要的一步。识别模型是否恰当需要有一个可以比较的标准，这里给出的标准是：对一般ARMA模型体系中的一些特征，分析其理论特征，把这种特定模型的理论特征作为鉴别实际模型的标准，观测实际用水资料与理论特征的接近程度。最后，根据这种分类比较分析的结果，来判定实际模型的类型。

第二阶段：用用水时间序列的数据，估计模型的参数，并进行检验，以判定该预测模型是否恰当。如不恰当，则返回第一阶段，重新选定模型。这个阶段是博克斯—詹金斯法中复杂繁琐的一步。然而在计算机及计算方法高度发展的今天，繁琐的计算过程在电子计算机的帮助下便成为一件轻而易举的事情了。借助于统计分析软件包，如EViews、TSP、SPSS等，我们可以方便的在计算机上实现对ARMA模型的估计，并对模型进行检验。

第三阶段：当一个恰当的模型选定后，对将来的某个时期的需水量作出预测。